Признаки сходимости рядов.
Необходимый признак сходимости ряда: последовательность членов сходящегося ряда должна стремится к нулю: 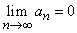 .
.
Это условие не является достаточным, как показывает пример ряда 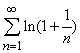 .
.
Для этого ряда выполняется необходимый признак сходимости ряда: 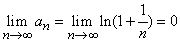 , однако, ряд расходится, так как частичные суммы
, однако, ряд расходится, так как частичные суммы
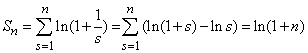 неограниченно возрастают.
неограниченно возрастают.
Для выяснения сходимости рядов найдены разнообразные достаточные признаки сходимости или расходимости рядов.
Признак Д'Аламбера:если существует такое положительное c < 1, что начиная с некоторого n, выполняется неравенство 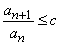 ,
,
то ряд сходится. Если же начиная с некоторого n, выполняется неравенство 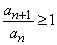 ,
,
то ряд расходится. Отсюда, в частности, следует сходимость геометрической прогрессии при знаменателе 0 < q < 1и расходимость приq 1.
ПризнакКоши:если существует такое положительное c < 1, что, начиная с некоторого n, выполняется неравенство: 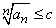 ,
,
то ряд сходится. Если же, начиная с некоторого n, выполняется неравенство: 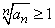 ,
,
то ряд расходится.
Особое место среди рядов занимают такие, в которых знаки слагаемых строго чередуются, а абсолютные величины рядов монотонно убывают. Оказывается, для таких рядов необходимый признак сходимости ряда является одновременно и достаточным, т.е., если 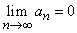 , то ряд
, то ряд 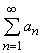 сходится.
сходится.
ВОПРОС 52. Достаточные признаки сходимости знакопостоянных рядов.
1) A= 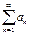 , B=
, B= 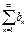
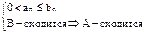
Для доказательства применим критерий Коши:
| am+1+…+an | = am+1+am+2+…+an≤bm+1+bm+2+…+bn<e
Предельный
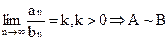
Доказательство: из существования предел 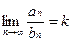 следуют неравенства:
следуют неравенства:
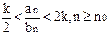
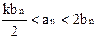 тогда по признаку сравнения (1) ряд сходится.
тогда по признаку сравнения (1) ряд сходится.
Пример.
z(α)= 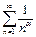 , рассмотрим как ведёт себя этот ряд в зависимости от α. При α=1 ряд расходится (гармонический). Было доказано ранее.
, рассмотрим как ведёт себя этот ряд в зависимости от α. При α=1 ряд расходится (гармонический). Было доказано ранее.
Для α<1 => 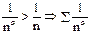 расходится по признаку сравнения 1.
расходится по признаку сравнения 1.
Для α>1
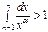 тогда по теореме о среднем выполняются неравенства
тогда по теореме о среднем выполняются неравенства
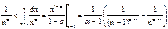
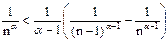
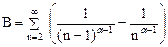
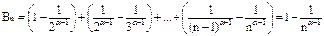
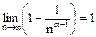 , т.е. В – сходится, значит по признаку сравнения z(α) при α>1 то же сходится.
, т.е. В – сходится, значит по признаку сравнения z(α) при α>1 то же сходится.
Таким образом
z(α) = 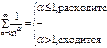
ВОПРОС 53. Знакопеременные и знакочередующиеся числовые ряды. Ряд Лейбница.
два частных случая числовых рядов - это знакопеременные и знакочередующиеся ряды.
Определение 3. Ряд называется знакочередующимся, если он имеет вид:
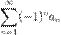 (или
(или 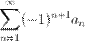 ), где
), где 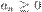 .
.
Ряды, не являющиеся знакопостоянными ( 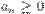 или
или 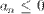 ) называются знакопеременными.Например,
) называются знакопеременными.Например, 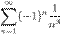 - знакочередующийся ряд,
- знакочередующийся ряд, 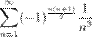 - знакопеременный ряд.
- знакопеременный ряд.
Признак Даламбера и оба признака Коши в случае знакопеременных и знакочередующихся рядов не работают!
Определение 4. Ряд 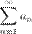 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 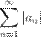 сходится.
сходится.
Определение 5. Ряд называется условно сходящимся, если он сходится, но не является абсолютно сходящимся.
Ряд Лейбница
Ряд вида
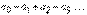 , (1)
, (1)
где числа 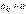 , монотонно убывая, стремятся к нулю
, монотонно убывая, стремятся к нулю 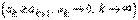 , называется рядом Лейбница.
, называется рядом Лейбница.
Покажем, что ряд Лейбница сходится и его сумма 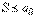 .
.
В самом деле, частичная его сумма 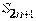 с нечетным номером
с нечетным номером 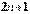 может быть записана в виде
может быть записана в виде
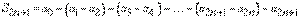 ,
,
откуда, очевидно, следует, что она ограничена сверху числом 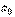 :
:
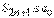 . С другой стороны, она может быть записана в виде
. С другой стороны, она может быть записана в виде
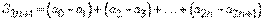 ,
,
откуда следует, что она монотонно не убывает. Но в таком случае существует предел
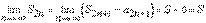 .
.
Теорема доказана.
ВОПРОС 54.Степенной ряд. Теорема Абеля. Радиус (интервал) сходимости степенного ряда.
Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
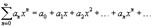
Часто рассматривается также ряд, расположенный по степеням (x − x0), то есть ряд вида
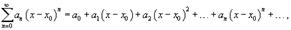
где x0 − действительное число.
Интервал и радиус сходимости
Рассмотрим функцию 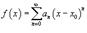 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
Если интервал сходимости представляется в виде 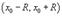 , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
, где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
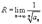
или на основе признака Даламбера:
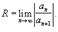
Теорема Абеля
Если степенной ряд (30.2) сходится при 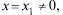 то он абсолютно сходится
то он абсолютно сходится 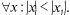 Если ряд (30.2) расходится в т.
Если ряд (30.2) расходится в т. 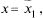 то он расходится
то он расходится 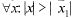
Пусть ряд 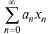 сходится, тогда
сходится, тогда 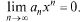 Поскольку
Поскольку
функция, имеющая предел, ограничена, то 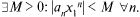 Перепишем ряд (30.2) в виде
Перепишем ряд (30.2) в виде
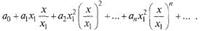
Для ряда из абсолютных величин его членов
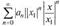 (30.3)
(30.3)
имеем 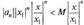 > причем геометрическая прогрессия
> причем геометрическая прогрессия 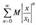 сходится при
сходится при 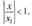 Таким образом, при
Таким образом, при 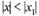 по первому признаку сравнения ряд (30.3) сходится, тогда по признаку абсолютной сходимости ряд (30.2) сходится абсолютно.
по первому признаку сравнения ряд (30.3) сходится, тогда по признаку абсолютной сходимости ряд (30.2) сходится абсолютно.
Пусть теперь ряд (30.2) расходится при 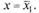 Предположим в противоречие с утверждением теоремы, что
Предположим в противоречие с утверждением теоремы, что 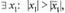 при котором ряд (30.2) сходится. Но по доказанному выше ряд (30.2) должен тогда сходиться в т.
при котором ряд (30.2) сходится. Но по доказанному выше ряд (30.2) должен тогда сходиться в т. 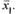 Полученное противоречие с условием доказывает теорему
Полученное противоречие с условием доказывает теорему
ВОПРОС 55. Ряды Тейлора и Маклорена. Разложения важнейших элементарных функций в степенной ряд.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
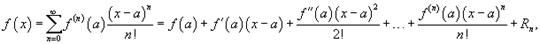
где Rn − остаточный член в форме Лагранжа определяется выражением
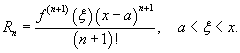
Если приведенное разложение сходится в некотором интервале x, т.е. 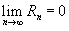 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена:
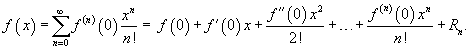
Разложение некоторых функций в ряд Маклорена
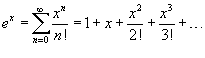
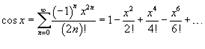
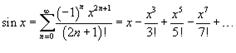
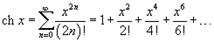
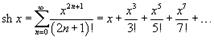
Дата добавления: 2016-07-18; просмотров: 2376;










