Операции над множествами

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой)множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}

2 Важнейшие числовые системы (натуральные, целые, рациональные и вещественные числа).

1.Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).

Существуют два подхода к определению натуральных чисел — числа, используемые при:

§ перечислении (нумеровании) предметов (первый, второй, третий, …);

§ обозначении количества предметов (нет предметов, один предмет, два предмета, …). Принят в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств.

Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются.

ВОПРОС 2. Важнейшие числовые системы (натуральные, целые, рациональные и вещественные числа).

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N ={1,2,3,....}

Целые числа – это числа из множества {0, 1, -1, 2, -2, ....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, чтоZ={1,2,3,....}.

Рациональные числа – это числа, представимые в виде дроби 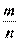, где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести: , , .

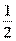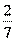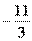Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это , , .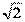

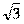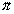Любое действительное число можно отобразить на числовой прямой:

Для перечисленных выше множеств чисел справедливо следующее высказывание:

То есть множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. А множество рациональных чисел входит во множество действительных чисел. Это высказывание можно проиллюстрировать с помощью кругов Эйлера.

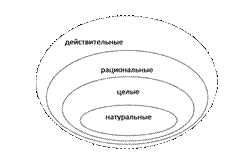
Основные числовые системы — арифметика натуральных чисел, кольцо целых рациональных чисел, кольцо полиномов, поле рациональных чисел, поле вещественны Алгебраической системой

Числовые системы

Делимость чисел

Пусть a , b ∈ Z. Число a делится на число b (a кратно b), если найдётся такое число

q ∈ Z, что a = q * b.

Отношение делимости b | a (b делит a), заданное на N, является рефлексивным,

антисимметричным и транзитивным, т.е. отношением частичного порядка.

Наибольшее (наименьшее) целое число,

на которое делятся (которое делится на)

заданные целые числа a , b , c , …, n ∈ Z называется их

наибольшим общим делителем – НОД (наименьшим общим кратным – НОК)

и обозначается ( a , b , c , …, n ) для НОД, [ a , b , c , …, n ] для НОК.

Если ( a , b , c , …, n ) = 1 ,

то числа a , b , c , …, n называются взаимно простыми.

Количество чисел ряда 0 , 1 , 2 , … , a – 1 взаимно простых с числом a

называется функцией Леонарда Эйлера, которая обозначается ϕ (a)

ТЕМА IV. ЧИСЛОВЫЕ СИСТЕМЫ
1. Множество натуральных чисел
Определение: Множество называется числовым, если его элементами являются
числа.
Известны следующие числовые системы:
N - множество натуральных чисел;
Z - множество целых чисел;
Q - множество рациональных чисел;
R - множество действительных чисел;
С - множество комплексных чисел.
Между этими множествами установлены следующие отношения:N ( Z ( Q ( R ( C.
В основе расширения числовых множеств лежат следующие принципы: если
множество А расширяется до множества В, то:
1) А ( B;
2) операции и отношения между элементами, выполнимые во множестве А,
сохраняются и для элементов множества В;
3) во множестве В выполняются операции, не выполнимые или частично
выполнимые во множестве А;
4) множество В является минимальным расширением множества А, обладающим
свойствами 1) – 3).
Множество натуральных чисел N строго определяется с помощью аксиом
Пеано.
1. Существует натуральное число 1, не следующее ни за каким натуральным
числом (натуральный ряд начинается с 1).
2. Каждое натуральное число следует только за одним и только одним
натуральным числом (в натуральном ряду нет повторений).
3. За каждым натуральным числом следует одно и только одно натуральное
число (натуральный ряд бесконечен).
4. Аксиома индукции. Пусть М ( N. Если:
1) 1 ( М;
2) ( а ( М множеству М принадлежит и следующий за а элемент а1 то
множество М совпадает с множеством натуральных чисел.
Итак, множество N = { 1, 2, 3, 4,...}.
На аксиоме 4 основан метод математической индукции. Доказательство
различных утверждений этим методом проводится от частного к общему, а
затем делается вывод о справедливости данного утверждения.
2. Множество целых чисел
Во множестве натуральных чисел выполняются операции сложения и
умножения, но не всегда выполняется операция вычитания. Расширяя
множество N так, чтобы эта операция была выполнима, мы получаем
множество целых чисел Z. Поэтому Z=N ( {0, -1, -2,...} или Z={...-3, -2,
-1, 0, 1, 2, 3,...}, т.е. множество целых чисел Z содержит множество
натуральных чисел, число нуль и числа, противоположные натуральным.
Основную роль во всей теории целых чисел играют следующие факты.
Т е о р е м а о д е л е н и и с о с т а т к о м. Для любого целого а
и b > 0 существуют и притом единственные целые q и r, такие, что а = bq
+ r, 0 ( r < | b |.
О п р е д е л е н и е. Натуральное число р называется простым, если р >
1 и р не имеет положительных делителей, отличных от 1 и р.
называется каноническим.
О п р е д е л е н и е. 1) Общим делителем целых чисел а1, а2, ..., аn
называется целое число d, такое, что a1 : d, а2 : d, ..., аn : d. 2)
Наибольшим общим делителем целых чисел а1, а2, ..., аn называется такой
положительный общий делитель чисел а1, а2, ..., аn, который делится на
любой другой общий делитель этих чисел.Обозначается: d = (а1, а2, ..., аn).
Наибольший общий делитель целых чисел а и b может быть найден с помощью
алгоритма Евклида, в основе которого лежит теорема о делении с остатком.
Последний, отличный от нуля, остаток и будет наибольшим общим делителем
чисел а и b.
О п р е д е л е н и е. Наименьшим общим кратным целых чисел а1, а2, ...,
аn, отличных от нуля, называется наименьшее положительное число, кратное
всем этим числам.Обозначают: m=[ а1, а2, ..., аn].
3. Множество рациональных чисел. Система действительных чисел
, m, n ( Z, n(0}. Множество рациональных чисел можно еще определить как
множество бесконечных периодических десятичных дробей.
Если же число нельзя представить в виде отношения двух целых чисел, то
его называют иррациональным числом. = 0,333 ... = 0,(3).
Множество, состоящее из всех рациональных и всех иррациональных чисел,
называется множеством действительных чисел R. Геометрически
действительные числа изображаются точками числовой прямой. Отметим, что
между множеством действительных чисел и множеством точек числовой прямой
установлено взаимно однозначное соответствие.
4. Система комплексных чисел
Однако действительных чисел недостаточно для того, чтобы решить любое
квадратное уравнение с действительными коэффициентами. Например,
уравнение вида х2 + 1= 0 действительных корней не имеет. А это означает,
что система действительных чисел нуждается в расширении.
О п р е д е л е н и е. Множество чисел вида а + bi, а, b ( R, i2 = -1,
называется системой комплексных чисел С.
- мнимая единица, b - коэффициент при мнимой единице. Запись числа в
виде z = а + bi называется алгебраической. Комплексное число z = а + bi
равно нулю тогда и только тогда, когда а = 0 и b = 0. Два комплексных
числа z1 = а1 + b1i и z2 = а2 + b2i называются равными, если а1 = a2, и
b1 = b2, в этом случае пишут: z1 = z2.
называются взаимно сопряженными. Например, числа z = 2 + i и z = 2 - i;
z = -5 - i и z = -5 + i, z = i и z = -i будут взаимно сопряженными.

= a2+b2..
Геометрически комплексные числа можно изображать точками плоскости,
абсциссами которых служат действительные части, а ординатами -
коэффициенты при мнимой единице. Таким образом, если z= a+bi, то на
плоскости ХОУ это будет точка М(а, b). Так как любой вектор плоскости с
началом в точке O(0,0) определяется координатами конца, то комплексные
числа также изображают радиус – векторами
Кроме алгебраической формы комплексное число может быть записано с
помощью тригонометрической формы. Введем следующие определения.
Возьмем на плоскости точку М(а, b), пусть ей соответствует комплексное
число z = а + bi. Обозначим через ( угол, который образует радиус –
вектор ОМ с положительным направлением оси ОХ.
= г, ОА =а; AM =b; тогда z = а + bi = rcos( + irsin( = r(cos( + isin().
Запись числа z = r(cos( + isin() называется тригонометрической формой
комплексного числа.

ВОПРОС 3.Важнейшие математические структуры (пространство n измерений. Метод координат).

Большую роль в развитии геометрии сыграло применение алгебры к изучению свойств геометрических фигур, разросшееся в самостоятельную науку — аналитическую геометрию. Возникновение аналитической геометрии связано с открытием метода координат, являющегося основным ей методом.

Координатами точки, называются числа, определяющие положение точки на данной линии или на данной поверхности или же в пространстве. Так, положение точки на земной поверхности будет определено, если известны её географические координаты — широта и долгота.

Для нахождения координат точки необходимо задание ориентиров, от которых ведётся отсчёт. В случае географических координат такими ориентирами будут экватор и нулевой меридиан.

Если даны ориентиры и указано, как, пользуясь ими, находить координаты точки, то говорят, что задана система координат.

Характерной особенностью метода координат является определение геометрических фигур уравнениями (см. § 4), что позволяет производить геометрические исследования и решать геометрические задачи средствами алгебры.

Придавая геометрическим исследованиям алгебраический характер, метод координат переносит в геометрию наиболее важную особенность алгебры — единообразие способов решения задач. Если в арифметике и элементарной геометрии приходится, как правило, искать для каждой задачи особый путь решения, то в алгебре и аналитической геометрии решения проводятся по общему для всех задач плану, легко приспособляемому к любой задаче. Можно сказать, что аналитическая геометрия занимает такое же положение по отношению к элементарной геометрии, какое алгебра занимает относительно арифметики. Перенесение в геометрию свойственных алгебре и поэтому обладающих большой общностью способов решения задач составляет главную ценность метода координат. Следует, однако, предостеречь читателя от пренебрежительного отношения к приёмам элементарной геометрии, так как в отдельных случаях они позволяют находить изящные решения, более простые, чем получаемые методом координат.

Другое достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.

При практическом применении понятия координат координаты предмета, рассматриваемого условно как точка, могут быть определены лишь приближённо. Задание координат предмета означает, что точка, определяемая этими координатами, либо является одной из точек этого предмета либо достаточно близка к нему.

Размеры и назначение книжки обязывают нас ограничиться сообщением начальных сведений о методе координат и простейших его приложениях. Много внимания уделено нами вопросу определения геометрических фигур уравнениями, обычно затрудняющему учащегося при первом ознакомлении с методом координат. Разъяснение этого вопроса иллюстрировано детально рассмотренными примерами.

ВОПРОС 4. Линейное пространство и его важнейшие свойства.

Аксиоматика линейных пространств.

Определение.Линейным пространством L = {a,b,c,…}называется множество, относительно элементов которого определены операции сложения и умножения на число, причем результаты этих операций принадлежат этому же множеству (говорят, что L замкнуто относительно операций сложения и умножения на число): .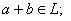

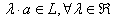(Элементы линейных пространств также будем называть векторами)

Для 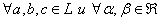эти операции удовлетворяют следующим условиям:

1. a + b = b + a (коммутативность сложения).

2. (a + b) + c = a + (b + c) (ассоциативность сложения).

3. .

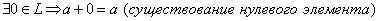4.

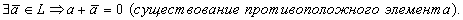
5. 1·а = а.

6.

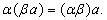
7. (α + β)а = αа + βа (дистрибутивность).

8. α(а + b) = αa + αb (дистрибутивность).

Перечисленные свойства, обычно, называют аксиомами. Имеют место теоремы:

Теорема 1. Нулевой элемент – единственен.

{От противного: 0₁,0₂; 0₁+0₂=0₁ и 0₂+0₁=0₂ (акс. (3)). Из акс.(1) следует: 0₁=0₂}

Теорема 2. 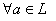противоположный элемент – единственен.

{Пусть для }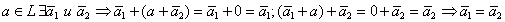

Теорема 3. 0·а = 0.

{ }

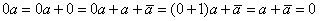Теорема 4.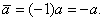

{ }

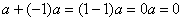Примеры.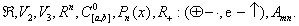

§2. Линейно зависимые и линейно независимые системы элементов.

Определение 1. Сумма 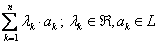называется линейной комбинацией элементов а₁, а₂,…,а_n с коэффициентами λ_k .

Определение 2.Система элементов линейного пространства {a₁,…,a_n} называется линейно зависимой, если найдутся коэффициенты λ₁,…,λ_n не все равные нулю, линейная комбинация с которыми равна нулю, т.е.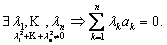

Определение 3.Система элементов линейного пространства {a₁,…,a_n} называется линейно

независимой, если ее линейная комбинация равна нулю только с нулевыми коэффициентами: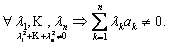

Имеют место несколько простых утверждений.

Теорема 1(необходимое и достаточное условие линейной независимости). a₁,…,a_n – линейно зависима 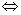когда хотя бы один из элементов является линейной комбинацией остальных.

Теорема 2.Если один из элементов системы равен нулю, то вся система линейно зависима.

{ }

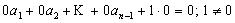Теорема 3. Если подсистема линейно зависима, то и вся система линейно зависима.

{ }

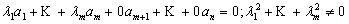Евклидовы пространства.

Определение 1.Линейное пространство E = {f, g, h, …} называется евклидовым, если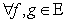

ставится в соответствие число, называемое скалярным произведением: 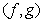. При этом, для 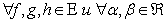выполняются аксиомы:

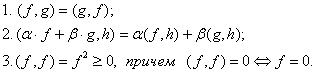
§8.Линейные операторы.

Определение 1. Функция (отображение) А, определенная на линейном пространстве L_n , область значений которой принадлежит линейному пространству L_m (здесь n и m – размерности соответствующих пространств) называется оператором :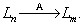

Если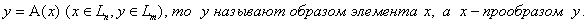

Все прообразы нулевого элемента L_m называют ядром оператора А: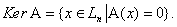

Определение 2. Оператор А называется линейным, если для 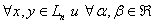выполняется равенство: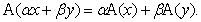

Определение 3.Матрицей линейного оператора А называется матрица (будем обозначать ее через А_mn ), столбцами которой являются координаты образов базисных элементов {e} в базисе {f}, т.е. , если

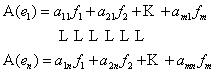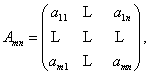, то или в матричной форме:

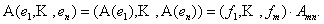
Замечание. Оператор, в частности линейный, определяет некоторое действие на элементы линейного пространства и не зависит от базиса. В свою очередь, матрица линейного операторазависит как от базиса пространства прообразов, так и от базиса пространства образов.

Теорема 1.Образ вектора х равен произведению матрицы линейного оператора на столбец его координат: если у = А(х), то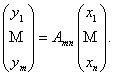

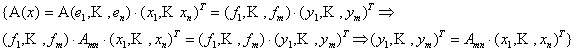
Таким образом, каждому линейному оператору ставится в соответствие матрица. Верно и обратное: каждой матрице можно поставить в соответствие линейный оператор. {Зададим оператор А формулой

}

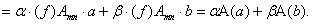В настоящем курсе используются операторы, прообразы и образы которых принадлежат одному и тому же линейному пространству L . Матрицы таких операторов квадратные, а образы и прообразы, естественно, представляются в едином базисе. Будем обозначать матрицу оператора А как A_n (n – размерность пространства), либо A_e ( {e} - базис пространства). В дальнейшем будем рассматривать только такие операторы.

Одной из особенностей этих операторов является наличие определителя у его матрицы.

Определение 4.Линейный оператор из L в L , определитель матрицы которого равен нулю, называется вырожденным и невырожденным в противном случае.

Замечание. Матрицу невырожденного оператора можно рассматривать как матрицу перехода от одного базиса к другому.

Теорема 2.При переходе к новому базису матрица линейного оператора меняется по следующему закону: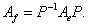

{Пусть {f} – новый базис, {e} – старый. 1) 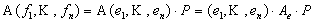(§5,8);

2) }

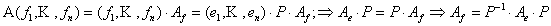Следствие. Определитель матрицы линейного оператора не зависит от базиса.

{ }

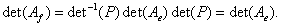Определение 4. Матрицы А и 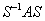называются подобными.

Свойства подобных матриц:

1. 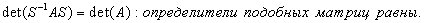{ см. выше}

2. 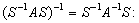матрица обратная к подобной подобна обратной матрице.

§9. Действия с линейными операторами.

Рассмотрим множество линейных операторов 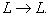Определим на этом множестве операции сложения, умножения на число и произведение операторов: А + В, λА и А·В.

1.

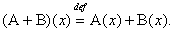
2.

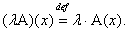
3.

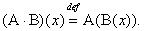
Легко проверить, что все указанные операторы – линейные. {проверим для А·В :

(АВ)(αх +βу) = А(αВ(х) + βВ(у)) = α(АВ)(х) +β(АВ)(у) }

Этим операторам соответствуют матрицы: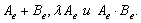

{ для двух первых действий – очевидно; (3): }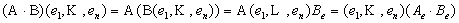

Свойства линейных операций:

1. А + В = В +А ; 5. λ( μА ) = (λμ)А ;

2. ( А + В ) + С = А + ( В + С ) ; 6. 1·А = А ;

3. А + Ø = А ; 7. (λ + μ)А = λА + μА ;

4. А + (−А ) = Ø ; 8. λ( А + В ) = λА + λВ ;

Из этих соотношений следует, что множество линейных операторов образует линейное пространство (размерности n² ).

Свойства произведения операторов:

1. (λА)·В = λ ( А·В) ; 3.( А + В )·С = А·С + В·С ;

2. А·( В·С ) = ( А·В )·С ; 4. А·( В + С ) = А·В + А·С ;

Произведение операторов позволяет ввести понятие степени оператора:

А¹ = А, А² = А·А и т.д. 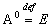(тождественному оператору: 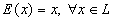, его матрица, очевидно, равна единичной). Так же, по определению, вводится понятие обратного

оператора: 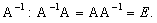Он обладает следующим свойством: если у = А(х),

то 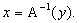Ясно, что его матрица равна обратной матрице исходного ( 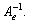) и он существует только у невырожденных операторов.

Пример.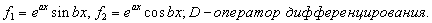

ВОПРОС 5. Линейная зависимость (независимость) элементов. Размерность и базис линейного пространства.

1. Линейно зависимые и независимые системы векторов.Определение. Система векторов 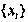называется линейно зависимой, если существует хотя бы одна нетривиальная линейная комбинация этих векторов, равная нулевому вектору. В противном случае, т.е. если только тривиальная линейная комбинация данных векторов равна нулевому вектору, векторы называются линейно независимыми.

Теорема (критерий линейной зависимости). Для того чтобы система век торов 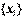линейного пространства была линейно зависимой, необходимо и достаточно, чтобы, по крайней мере, один из этих векторов являлся линейной комбинацией остальных.

1) Если среди векторов 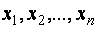имеется хотя бы один нулевой вектор, то вся система векторов линейно зависима.

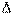В самом деле, если, например, 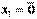, то, полагая 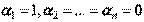, имеем нетривиальную линейную комбинацию .▲

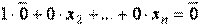2) Если среди векторов 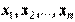некоторые образуют линейно зависимую систему, то и вся система 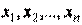линейно зависима.

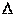Действительно, пусть векторы 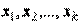, , 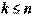линейно зависимы. Значит, существует нетривиальная линейная комбинация 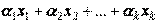, равная нулевому вектору. Но тогда, полагая 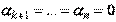, получим также нетривиальную линейную комбинацию 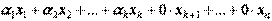, равную нулевому вектору.

2. Базис и размерность. Определение. Система линейно независимых векторов 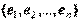векторного пространства 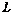называетсябазисом этого пространства, если любой вектор из 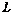может быть представлен в виде линейной комбинации векторов этой системы, т.е. для каждого вектора 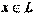существуют вещественные числа 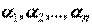такие, что имеет место равенство 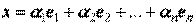Это равенство называется разложением вектора 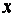по базису 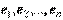, а числа 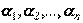называютсякоординатами вектора 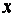относительно базиса (или в базисе) .

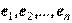Теорема (о единственности разложения по базису). Каждый вектор 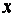пространства 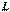может быть разложен по базису 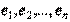единственным образом, т.е. координаты каждого вектора 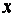в базисе 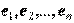определяются однозначно.

Главное значение базиса заключается в том, что операции сложения векторов и умножения их на числа при задании базиса превращаются в соответствующие операции над числами – координатами этих векторов. А именно, справедлива следующая

Теорема. При сложении двух любых векторов линейного пространства 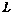их координаты (относительно любого базиса пространства) складываются; при умножении произвольного вектора на любое число 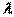все координаты этого вектора умножаются на .

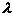Определение. Векторное пространство 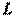называется 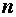-мерным, если в нем существуют 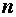линейно независимых векторов, а любые 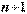векторов уже являются линейно зависимыми. При этом число 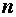называется размерностьюпространства .

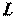Размерность векторного пространства, состоящего из одного нулевого вектора, принимается равной нулю.

Размерность пространства 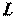обычно обозначают символом .

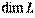Определение. Векторное пространство 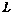называется бесконечномерным, если в нем существует любое число линейно независимых векторов. В этом случае пишут .

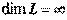Выясним связь между понятиями базиса и размерности пространства.

Теорема. Если 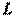– векторное пространство размерности 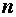, то любые 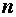линейно независимых векторов этого пространства образуют его базис.

Теорема. Если векторное пространство 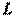имеет базис, состоящий из 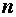векторов, то .

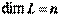ВОПРОС 6. Норма элемента, расстояние между элементами пространства. Ортонормированный базис.

Нормой называют функционал 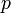, удовлетворяющий следующим аксиомам:

1. ,

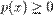2. ,

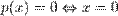3. 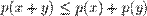(аксиома треугольника),

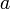4. для любого числа (абсолютная однородность).

Таким образом, норма - это полунорма, на которую наложено дополнительное условие: норма равна нулю только на нулевом элементе.

Нормированным пространством называют линейное пространство с заданной на нём нормой.

Норму элемента линейного пространства 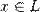обозначают .

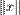Полное нормированное пространство называется банаховым пространством.

Евклидово пространство.Скалярным произведением в действительном линейном пространстве 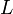называется функционал от двух переменных 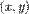, определённый для любых 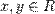и удовлетворяющий следующим аксиомам:

1. ,

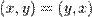2. ,

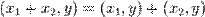3. ,

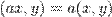4. ,

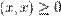5. .

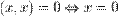Евклидово пространство — это линейное пространство с заданным в нём скалярным произведением.

В евклидовом пространстве норма естественным образом определяется через скалярное произведение: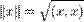

Ортогонализация — это процесс построения ортонормированной системы на основе линейно независимой системы векторов.

Теорема 1 (Об ортогонализации). Рассмотрим линейно независимую систему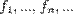

элементов евклидова пространства 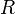. В пространстве 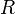существует ортогональная система элементов 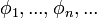, причём каждый элемент 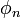есть линейная комбинация вида

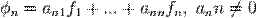,каждый элемент 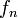представляется в виде 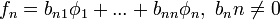,при этом, каждый элемент 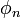определяется с точностью до множителя .

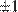ВОПРОС 7. Матрицы и основные действия над матрицами. Свойства действий над матрицами.

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называетсяквадратной.

Определение. Матрица вида:= E,называется единичной матрицей.

Определение. Если a_mn = a_nm , то матрица называется симметрической.

Определение.Квадратная матрица вида называется диагональнойматрицей.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij  b_ij С = А + В = В + А.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

 (А+В) =А  В А() = А  А

Операция умножения матриц

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам: AB = C;

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Свойства операции умножения матриц.

1)Умножение матриц не коммутативно, т.е. АВ  ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называютсяперестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

АЕ = ЕА = А

Очевидно, что для любых матриц выполняются следующее свойство: AO = O; OA = O,

где О – нулеваяматрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство: (АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно: А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа  верно соотношение: (AB) = (A)B = A(B).

5) Если определено произведение АВ , то определено произведение В^ТА^Т и выполняется равенство:(АВ)^Т = В^ТА^Т, где индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detAdetB.

ВОПРОС 8. Определители матриц. Основные свойства определителей.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании:

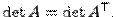
Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка. Непосредственная проверка доказывает данное свойство.

Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю.

Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.

Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.

Свойство 5. Если каждый элемент i-й строки (столбца) матрицы A представлен в виде суммы двух слагаемых, то определитель такой матрицы равен