Эмпирическое корреляционное отношение

Теснота или сила связи между двумя признаками может быть измерена показателем, называемым эмпирическим корреляционным отношением. Этот показатель назван эмпирическим, поскольку он может быть рассчитан на основе обычной группировки по факторному и результативному признаку, то есть на основе корреляционной таблицы. 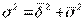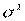Эмпирическое корреляционное отношение получается из правила сложения дисперсий, согласно которому , где - общая дисперсия; 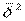- межгрупповая дисперсия; 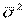- внутригрупповая (средняя из частных) дисперсия. Межгрупповая дисперсия является мерой колеблемости, обусловленной факторным признаком. Средняя из частных дисперсий является мерой колеблемости, обусловленной всеми остальными(кроме факторного) признаками. Тогда отношение 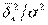выражает долю колеблемости, возникающей за счет факторного признака, в общей колеблемости. Квадратный корень из этого отношения и называется эмпирическим корреляционным отношением: .

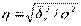Отсюда следует правило, что чем больше межгрупповая дисперсия, тем сильнее факторный признак влияет на вариации результативного признака. Составляющие отношения дисперсий вычисляются по данным корреляционной таблицы по следующим формулам:

; ,

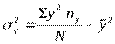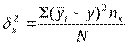где 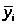- частные средние; 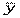- общая средняя; 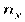- итоги по признаку 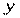; 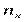- итоги по признаку 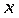; 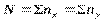- число наблюдений. То же соотношение сохраняется и для условных значений 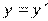, полученных числовым преобразованием .

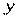Само отношение дисперсий (подкоренное выражение) называется коэффициентом детерминации (оно равно также квадрату эмпирического корреляционного отношения). Эмпирическое корреляционное отношение изменяется в широких пределах (от 0 до 1). Если оно равно нулю, значит факторный признак на корреляционный не влияет. Если 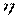=1, значит, результативный признак полностью зависит от факторного. Если же эмпирическое корреляционное отношение представляет дробь, близкую единице, то говорят о тесной связи между факторным и результативным признаками. Если эта дробь мала (близка нулю), то говорят о слабой связи между ними.