Коливання системи з двома ступенями вільності

Вільні коливання

Складемо рівняння Лагранжа другого роду для двохмасової системи, що зображена на рис.4.16:

рис. 4.16

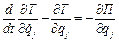; (j=1,2).

Ступінь вільності системи N=2 і , а , де

x₁– абсолютна координата руху маси т₁;

x₂ – абсолютна координата руху маси т₂.

Отже, маємо систему рівнянь

1) ;

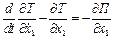2) .

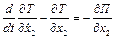Запишемо вирази для кінетичної та потенціальної енергій системи та знайдемо похідні необхідні для складання рівнянь руху:

; ; ; ;

;

; ; ; ;

;

;

.

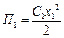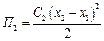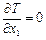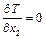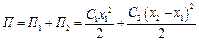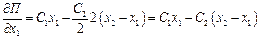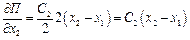Отримаємо систему рівнянь:

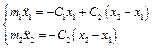, або .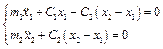

Поділивши почленно рівняння системи на відповідні маси одержимо:

.

Зробимо деякі заміни:

; ; ; ,

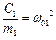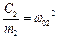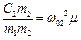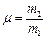де ω₀₁, ω₀₂ – парціальні частоти – частоти таких коливань системи, коли коливання за кожною з координат є незалежними (незв'язаними).

Звідси

Введемо оператор - 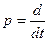, тоді

(*)

Для гармонічних процесів 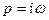, тобто

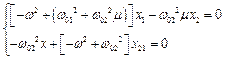(4.14)

Для того, щоб останнє рівняння мало нетривіальний розв'язок х₁≠0, х₂≠0, треба, щоб визначник матриці коефіцієнтів системи дорівнював нулю:

.

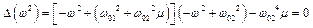Розкриваючи цей визначник, отримаємо рівняння частот, або, як його ще називають, вінове рівняння.

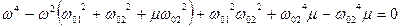
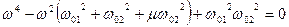
Розв'язками рівняння є два значення. Знайдемо їх графічно. Графік функції Δ(ω²) є параболою, гілки якої напрямлені вгору (рис.4.17). При ω²=0 Δ(0)>0, при ω²→∞ Δ(∞)=∞. Якщо частота ω² дорівнює квадрату однієї з парціальних частот, то

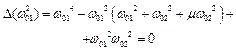
рис. 4.17

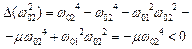
Із графіка Δ(ω²) випливає (рис.4.17), що обидва корені ω₁² і ω₂² характеристичного рівняння Δ(ω²)=0 додатні дійсні числа. Цей графік ілюструє теорему Релея про частоти власних коливань системи.

Теорема Релея

Найменша власна частота системи завжди менша найменшої парціальної частоти, а найбільша власна частота системи завжди більша від більшої парціальної частоти.

Розв'язок системи рівнянь, що описує коливання системи з двома ступенями вільності, дорівнюватиме лінійній комбінації розв'язків системи, що описує власні коливання:

; ,

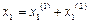або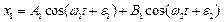

Знайдемо відношення з системи рівнянь (4.14):

; ;

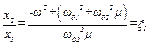Тепер загальний розв'язок для власних коливань двохмасової системи набуде вигляду:

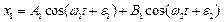
, де

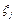–коефіцієнти форми коливань (показують у скільки разів амплітуда коливань n-ної маси більша (менша) від амплітуди коливань іншої маси, наприклад першої).

.

Ці коливання ( 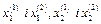), що відбуваються відповідно з частотою ω₁ і ω₂, називають головними коливаннями.

Нормальними (головними) координатами називають такі узагальнені координати, при яких кінетична енергія системи являє собою суму квадратів тільки узагальнених швидкостей.

Тоді, кінетична енергія у двохмасовій системі дорівнює

,

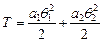де а₁, а₂ – маса для поступального руху, або момент для обертального руху;

θ₁, θ₂ – нормальні координати.

.

Запишемо рівняння Лагранжа другого роду в нормальних координатах для двохмасової системи

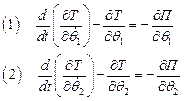
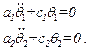
Розв'язок кожного з них має вигляд:

Зв'язок між узагальненими і нормальними координатами системи знаходиться з рівностей:

,

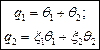де 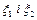- координати форми коливань.