Властивості визначеного інтеграла

І. Якщо 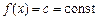, то

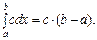
ІІ. Сталий множник можна виносити з-під знака визначеного інтеграла, тобто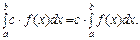

ІІІ. Якщо 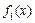та 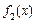інтегровні на [a; b], то

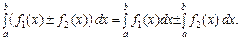
IV. Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл змінить лише свій знак на протилежний, тобто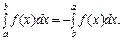

V. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю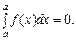

VI. Якщо 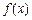— інтегровна в будь-якому із проміжків: [a; b], [a; c], [с; b], то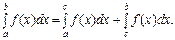

VII. Якщо 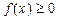і інтегровна для 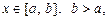то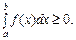

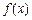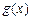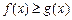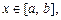
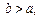VIII. Якщо , — інтегровні та для то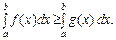

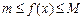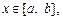
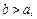IX. Якщо f(x) — інтегровна та для то

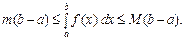
Доведення випливає як наслідок із властивостей І та VIII.

Х. Теорема 7 (про середнє).

Якщо функція 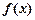— неперервна для 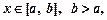то знайдеться така точка 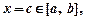що:

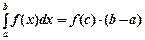(8.5)

Геометричний зміст теореми про середнє полягає в тому, що існує прямокутник із сторонами 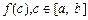та b – a, який рівновеликий криволінійній трапеції аАВв за умови, що функція 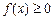та неперервна на проміжку [a; b] (рис. 7.6).

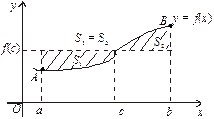
Рис. 8.3

Формула Ньютона—Лейбніца.

Розглянемо інтеграл 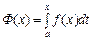, який буде функцією від верхньої межі інтегрування. Змінній х надамо приросту 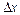, що зумовить приріст функції.

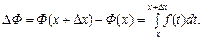(рис. 8.4)

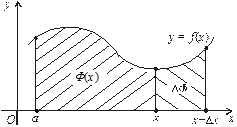
Рис. 8.4

Теорема 8. Якщо функція f(x) неперервна для будь-якого 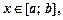то похідна від інтеграла зі змінною верхньою межею інтегрування по цій межі дорівнює підінтегральній функції від верхньої межі інтегрування, тобто

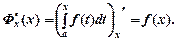(8.6)

Наслідки:

1. Визначений інтеграл зі змінною верхньою межею від функції 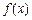є одна із первісних для .

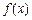2. Будь-яка неперервна функція на проміжку 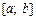має на цьому проміжку первісну, яку, наприклад, завжди можна побудувати у вигляді визначеного інтеграла зі змінною верхньою межею, тобто

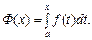
Приклад. Знайти .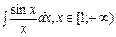

l Функція 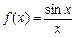— неперервна на проміжк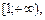у тому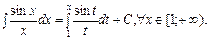

Теорема 9. (Ньютона—Лейбніца). Якщо функція 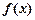— неперервна для 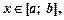то визначений інтеграл від функції 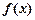на проміжку 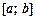дорівнює приросту первісної функції 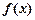на цьому проміжку, тобто

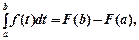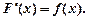де (8.7)

Позначимо дію подвійної підстановки так: 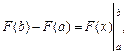тоді зв’язок між визначеним та невизначеним інтегралами можна подати такою рівністю:

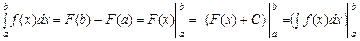(8.8)

Наслідок. Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральних функцій і виконати над нею подвійну підстановку.

Приклад.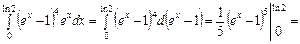

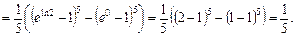
7. Обчислення площ плоских фігур в прямокутній системі координат.

Якою б не була криволінійна фігура, що обмежена неперервними кривими лініями, шляхом її розсікання лініями паралельними осям координат, обчислення площі фігури можна звести до обчислення площ розглянутих нижче фігур.

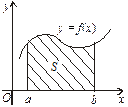
І. Фігура обмежена лініями 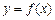, y = 0, x = a, x = b (рис. 8.5). Функція 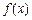— неперервна та 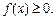Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така: .

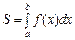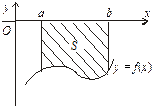
Якщо при виконанні всіх інших умов 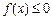(рис. 8.6),

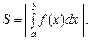(8.9)

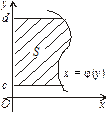
Рис. 8.5	Рис. 8.6	Рис. 8.7

ІІ. Фігура обмежена лініями 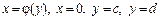(рис. 8.7). Функція 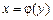— неперервна та 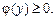Площа S такої фігури буде

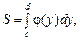(8.10)

<891011121314>

---

Дата добавления: 2016-05-26; просмотров: 3339;

---