Дифференциальные уравнения движения Навье–Стокса

При движении вязкой жидкости в потоке, кроме сил давления и тяжести, действуют также силы трения. Для трехмерного потока проекция равнодействующих сил трения на ось 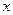имеет вид:

.

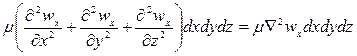Суммы проекций всех сил на оси координат должны быть равны произведению массы жидкости, заключенной в параллелепипеде, на проекции ускорения на оси координат:

;

;

.

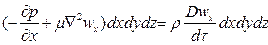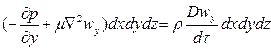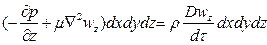После сокращения получим дифференциальные уравнения Навье – Стокса, описывающее движение вязкой капельной жидкости:

;

;

.

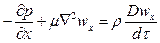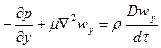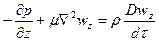Соответствующие субстанциональные производные в уравнениях могут быть выражены как для неустановившегося, так и установившегося течения жидкости.

Правые части уравнений выражают произведение массы единицы объема 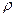на проекцию ускорения, т.е. представляют собой равнодействующие сил инерции, возникающих в движущейся жидкости.

В левых частях произведение 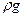отражает влияние сил тяжести, частные производные 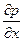, , 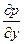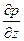- влияние сил гидростатического давления, а произведение вязкости на сумму вторых производных проекций скорости – влияние сил трения на движущую жидкость. Каждый член уравнения имеет размерность соответствующей силы, отнесенной к единице объема жидкости.

Полное описание движения вязкой жидкости возможно путем решения уравнений Навье–Стокса совместно с дифференциальным уравнением неразрывности потока. Однако уравнения Навье–Стокса не могут быть решены в общем виде.

Решение возможно либо для простых случаев при введении ряда допущений, либо после преобразования этих уравнений методами теории подобия.

Уравнение Бернулли

Решение уравнений движения Эйлера для установившегося потока жидкости приводит к одному из наиболее важных и широко используемых уравнений гидродинамики – уравнению Бернулли.

После умножения левых и правых частей дифференциальных уравнений на 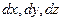и деления их на плотность жидкости 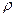получим

.

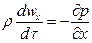
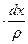
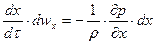
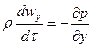
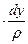
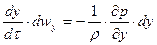
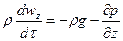
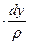
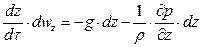Сложим эти уравнения, учитывая, что производные 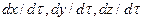выражают проекции 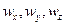скорости на соответствующие оси координат, и получим

.

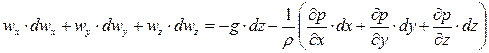Слагаемые левой части уравнения могут быть представлены как

, , ,

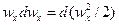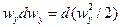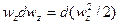а их сумма

.

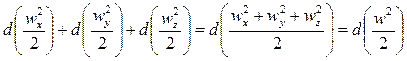В то же время сумма членов, стоящих в скобках в правой части записанного уравнения, представляет собой полный дифференциал давления 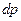(при установившихся условиях давление зависит лишь от положения точки в пространстве и не меняется со временем).

С учетом этих преобразований получим

.

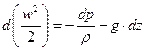Разделив обе части полученного уравнения на ускорение силы тяжести 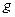и перенеся все члены в левую часть, найдем

.

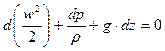Для несжимаемой изотермической жидкости 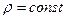сумма дифференциалов может быть заменена дифференциалом суммы

,

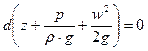тогда после дифференцирования

.

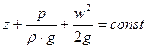Для любых двух поперечных сечений неразрывного потока жидкости уравнение имеет вид (рис. 2.10)

.

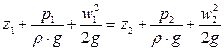Уравнение Бернулли описывает движение идеальной жидкости.

Величина 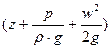представляет собой полный динамический напор.

Согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остается неизменной.

Гидродинамический напор включает три слагаемых, из которых первые два z и 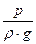входят в основное уравнение гидростатики и представляют собой: z – нивелирную высоту, называемую также геометрическим напором, представляющую удельную потенциальную энергию положения в данной точке;

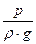– статический или пьезометрический напор характеризует удельную потенциальную энергию давления положения в данной точке;

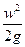– скоростной или динамический напор характеризует удельную кинетическую энергию в данной точке.

Таким образом, уравнение Бернулли имеет определенный энергетический смысл, состоящий в том, что при установившемся движении идеальной жидкости сумма удельной потенциальной 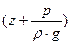и удельной кинетической 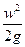энергий жидкости для каждого из поперечных сечений потока остается величиной неизменной.

При изменении поперечного сечения трубопровода и соответственно скорости движения жидкости происходит превращение энергии. При сужении трубопровода часть потенциальной энергии давления переходит в кинетическую, и, наоборот, при расширении трубопровода часть кинетической энергии переходит в потенциальную, но общее количество энергии остается постоянным.

Таким образом, уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока жидкости.

Для соблюдения баланса энергии при движении реальной жидкости в правую часть уравнения Бернулли должен быть введен член, выражающий потерянный напор. Тогда уравнение Бернулли для реальных жидкостей будет иметь вид

.

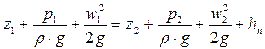Потерянный напор 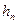характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении вязкой жидкости.

Если умножить обе части уравнения на 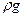, можно получить уравнение Бернулли в ином виде:

.

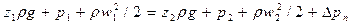В уравнении величина 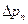– потерянное давление, равное

.

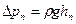Определение потерь напора или давления является практически важной задачей, связанной с расчетом энергии, необходимой для перемещения реальных жидкостей и газов при помощи насосов и компрессоров. Сложность решения этой задачи, как было сказано выше, обусловлена тем, что решение системы дифференциальных уравнений, описывающих движение реальной жидкости, в большинстве случаев оказывается невозможным.

Практические применения уравнения Бернулли. На практике уравнение Бернулли используется для определения скоростей (рис. 2.11) и расходов жидкостей и газов, напора насоса, времени истечения жидкостей из резервуаров. На рис. 2.12 приведена схема измерение расхода с помощью диафрагмы, на рис. 2.13 и 2.14 - с помощью сопла и трубы Вентури.

Рис. 2.11. Измерение скорости жидкости пневмометрической трубкой

Зависимость для определения объемного расхода жидкости через дроссельные устройства (диафрагму, мерное сопло, трубу Вентури) имеет вид:

,

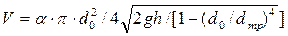где 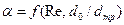– коэффициент расхода дроссельного прибора. Значения коэффициента определяются опытным путем и приводятся в специальной литературе; 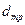– диаметр трубопровода; 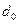– диаметр наиболее узкого сечения мерного устройства.

Объемный расход жидкости при истечении через круглое отверстие в днище сосуда с постоянным уровнем 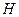жидкости:

.

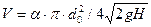Из уравнения следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда (рис. 2.15).

С помощью уравнения Бернулли можно также определять время опорожнения сосуда от жидкости, имеющего постоянное поперечное сечение, от высоты 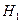до :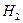

,

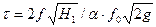а также решать другие прикладные задачи, например, вычислять напор насоса.