Приложения кратных интегралов

Понятие о кратных интегралах

Двойные интегралы

Пусть функция z=f(x,y)определена и непрерывна в ограниченной замкнутой области D плоскости O_xy. Разобьем область D произвольным образом на n областей S₁, S₂, … , S_n , которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке: , , которые назовем точками пунктуации. Обозначим через - площадь, через - диаметр i-ойэлементарной области (i=1,…, n), . Составим выражение

(1)

Выражение (1) называется интегральной суммой Римана для функции z=f(x,y)по области D. Заметим, что она зависит от способа разбиения области D на элементарные области и от способа выбора точек пунктуации.

Если существует предел интегральной суммы Римана (1) при , и этот предел не зависит ни от способа разбиения области на элементарные области, ни от выбора точек пунктуации, то он называется двойным интегралом от функции z=f(x,y)по области D и обозначается

Таким образом,

(2)

Свойства двойных интегралов аналогичны свойствам определенных интегралов. Отметим два, наиболее часто используемых на практике, свойства.

1) Свойство линейности. Если функции f(x,y)и g(x,y) интегрируемы по области D, то справедлива формула:

2) Свойство аддитивности. Если область D разбита на две области D₁ и D₂ без общих точек, и функция f(x,y)интегрируема во всех точках области D, то справедлива формула:

Вычисление двойных интегралов сводится к вычислению повторных интегралов следующим образом. Пусть область D ограничена слева и справа вертикальными прямыми x=a, x=b, а снизу и сверху – кривыми ,причем - непрерывны и на промежутке [a,b](Рис.1).Такую область назовем правильной в направлении оси Oy. Тогда

, (3)

причем сначала вычисляется интеграл по переменной y (x - параметр), а полученный результат интегрируется по x .

Рис.1.

Заметим, что если кривая (или ) на промежутке [a,b]задается различными аналитическими выражениями, например,

,

то интеграл справа в (3) записывается в виде суммы двух интегралов:

.

Аналогично, пусть область D ограничена снизу и сверху горизонтальными прямыми y=c, y=d, а слева и справа - кривыми , причем непрерывны и на промежутке [c,d](Рис.2). Такую область назовем правильной в направлении оси Ox. Тогда

(4)

Рис. 2

Теорема(о замене переменных в двойном интеграле)

Пусть выполняются условия:

1) функции x=x(u,v) и y=y(u,v)таковы, что каждой точке с координатами (x, y) из области D соответствует единственная точка с координатами (u, v) из области D₁ и наоборот;

2) функции x=x(u,v) и y=y(u,v)имеют непрерывные частные производные по переменным u и v в области D₁;

3) функция z=f(x,y) определена и интегрируема в области D.

Тогда справедлива формула:

, (5)

где

- якобиан перехода от декартовых координат к криволинейным координатам.

Частным случаем криволинейных координат для двойного интеграла являются полярные координаты:

,

для которых якобиан равен и формула (5) примет вид:

(6)

Задание 1. Вычислить повторный интеграл: .

Решение. Вычислим сначала интеграл по переменной y (x - параметр). Имеем

.

Полученный интеграл является обычным определенным интегралом. Окончательно имеем

.

Задание 2. Записать данный двойной интеграл в виде повторных, взятых в различных порядках:

,

область интегрирования D ограничена линиями x=2, y=x, y=1/x.

Решение. Построим область интегрирования D (рис.3).

1)По формуле (3) при a=1, b=2, получаем

.

Рис. 3.

2) Если же для вычисления данного интеграла применить формулу (4), то надо положить c=1/2, d=2, , .

Тогда

.

Задание 3. Изменить порядок интегрирования в повторном интеграле:

.

Решение. Область интегрирования D ограничена снизу кривой

,

сверху кривой

и представлена на рис. 4.

Рис. 4.

Поэтому имеем

.

Задание 4. Перейдя к полярным координатам, вычислить интеграл:

.

Решение. Положим

и применим формулу (6). Так как , то

.

Областью интегрирования исходного интеграла является четверть круга радиуса R=1 с центром в начале координат (рис. 5).

Рис. 5.

Следовательно, в области D₁ изменяется от 0 до 1 и . Таким образом, имеем:

.

Тройные интегралы

Пусть функция u=f(x,y,z) определена и непрерывна в ограниченной замкнутой области T пространства O_xyz. Разобьем область T произвольным образом на n областей V₁, V₂,…, V_n, которые назовем элементарными областями. В каждой из элементарных областей произвольным образом выберем по точке , которые назовем точками пунктуации. Обозначим через объем, а через диаметр i-ойэлементарной области (i=1,…,n), . Составим выражение

, (7)

которое называется интегральной суммой Римана для функции u=f(x,y,z) по области T . Заметим, что выражение (7) зависит от способа разбиения области T на элементарные области и от способа выбора точек пунктуации.

Если существует предел выражения (7) при и если этот предел не зависит ни от способа разбиения области T на элементарные области, ни от способа выбора точек пунктуации, то он называется тройным интегралом от функции u=f(x,y,z) по области T и обозначается

Таким образом,

(8)

Свойства тройных интегралов аналогичны свойствам двойных интегралов.

Вычисление тройных интегралов сводится к вычислению повторных интегралов следующим образом. Пусть область T ограничена снизу поверхностью , сверху поверхностью и с боков прямой цилиндрической поверхностью; проекцией области T на плоскость O_xy является область D (рис. 6). Такую область назовем правильной в направлении оси Oz.

Рис. 6

Пусть функция u=f(x,y,z) определена и интегрируема в области T и для любых точек существует интеграл

.

Тогда существует интеграл

и справедлива формула

(9)

Аналогичные формулы справедливы и в случае, когда область T правильная в направлении оси Ox или оси Oy .

Теорема (о замене переменных в тройном интеграле). Пусть выполняются следующие условия:

1) функции x=x(u,v,w), y=y(u,v,w) и z=z(u,v,w) таковы, что каждой точке с координатами (x,y,z) из области T соответствует единственная точка с координатами (u,v,w) из области T₁ и наоборот;

2) функции x=x(u,v,w), y=y(u,v,w) и z=z(u,v,w) имеют непрерывные частные производные по переменным u , v и w;

3) функция u=f(x,y,z) определена и интегрируема в области T .

Тогда справедлива формула:

, (10)

где

- якобиан перехода от декартовых координат к криволинейным координатам.

Частным случаем криволинейных координат для тройного интеграла являются цилиндрические и сферические координаты.

1) В случае цилиндрических координат положение точки M в пространстве определяется тремя числами , где и - полярные координаты проекции точки M на координатную плоскость O_xy, z – аппликата точки M (рис.7).

Рис. 7

Имеют место формулы:

,

якобиан перехода от декартовых координат к цилиндрическим равен и формула (10) принимает вид:

(11)

2) В случае сферических координат положение точки M в пространстве определяется тремя числами , где - расстояние от начала координат до точки M, - угол между проекцией радиус-вектора точки M на плоскость O_xy и осью Ox, - угол между радиус-вектором точки M и осью Oz (рис.8).

Рис. 8

Имеют место формулы:

,

якобиан перехода от декартовых координат к сферическим равен 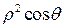и формула (10) принимает вид:

(12)

Задание 1. Вычислить интеграл:

,

где T - тетраэдр, ограниченный плоскостями: x+y+z=1, x=0, y=0, z=0.

Решение. Изобразим область интегрирования (рис.9).

Область интегрирования ограничена снизу плоскостью z=0, сверху плоскостью z=1-x-y, по бокам плоскостями x=0 и y=0. Проекцией области T на плоскость O_xy является область D - треугольник OAB . По формуле (9) имеем:

.

Рис. 9

Записывая двойной интеграл по области D через повторный интеграл, получим:

И, наконец, вычислим полученный повторный интеграл:

.

Задание 2. Перейдя к цилиндрическим координатам, вычислить интеграл:

.

Решение.Изобразим область интегрирования (рис.10).

Рис. 10

Положим

и применим формулу (11). Так как , то

Задание 3. Переходя к сферическим координатам, вычислить интеграл:

.

Решение. Область интегрирования T есть полушар (рис.11).

Рис. 11

Найдем пределы изменения сферических координат для области T₁:

Следовательно, по формуле (12) имеем:

.

Вычислив полученный тройной интеграл, получим:

.

Приложения кратных интегралов

1. Геометрические приложения двойных интегралов

Площадь S плоской области (фигуры) D выражается в зависимости от рассматриваемой системы координат, следующими интегралами:

(13)

- в декартовых координатах,

(14)

- в полярных координатах.

Пусть гладкая поверхность задана уравнением z=f(x,y). Тогда площадь части этой поверхности, проектирующейся в область D плоскости O_xy, равна:

(15)

Пусть область T ограничена снизу плоскостью z=0, сверху – непрерывной поверхностью z=f(x,y) и с боков прямой цилиндрической поверхностью. Если проекцией области T на плоскость O_xy является область D, то объем V области T выражается интегралом

(16)

2. Механические приложения двойных интегралов.

Масса M пластинки, занимающей область D плоскости O_xy , имеющей плотность , равна:

. (17)

Статические моменты M_x и M_y этойпластинки относительно осей Ox и Oy

выражаются интегралами:

(18)

Координаты центра масс и пластинки определяются следующим образом:

. (19)

Моменты инерции пластинки относительно осей Ox и Oy соответственно равны:

(20)

а момент инерции пластинки относительно начала координат равен:

. (21)

Заметим, что если рассматриваемая пластина однородна, то в приведенных формулах следует положить .

3. Геометрические приложения тройного интеграла

Объем V пространственной области T равен:

(22)

4.Механические приложения тройных интегралов. Масса M тела с плотностью ,занимающего область T, равна

(23)

Статические моменты M_xy, M_xz, M_yz тела относительно координатных плоскостей выражаются интегралами:

(24)

Координаты центра масс тела T определяются следующим образом:

. (25)

Моменты инерции тела относительно осей координат соответственно равны:

(26)

.

Заметим, что если рассматриваемое тело однородно, то в приведенных формулах следует положить .

Задание 1. Найти объем тела, ограниченного поверхностями:

.

Решение. Данное тело ограничено снизу плоскостью z=0, сверху плоскостью y+z=1 и с боков цилиндром (рис.12а).

Проекцией рассматриваемого тела является область D (рис. 12б).

Рис. 12а

Рис. 12б

Найдем объем нашего тела двумя способами:

1) с помощью двойного интеграла;

2) с помощью тройного интеграла.

В первом случае воспользуемся формулой (16). В нашем случае f(x,y)=1-y.

Следовательно,

.

Вычисляем полученный повторный интеграл:

V=8/15.

Теперь найдем значение объема данного тела с помощью тройного интеграла. Для этого воспользуемся формулой (22). Имеем:

.

Вычисляем полученный тройной интеграл:

V=8/15.

Задание 2. Найти координаты центра масс однородного тела, ограниченного поверхностями .

Решение. Данное тело изображено на рис.12а. Чтобы найти координаты центра масс рассматриваемого тела, воспользуемся формулами (25).

Найдем сначала массу тела. Для этого применим формулу (23) при , так как наше тело однородное. Имеем:

(это интеграл мы вычисляли в предыдущем примере).

Вычислим теперь статические моменты M_xy, M_xz, M_yz рассматриваемого тела относительно координатных плоскостей. Для этого воспользуемся формулами (24) при . Имеем:

,

,

Вычислив полученные тройные интегралы, имеем:

M_xy=16/105,

M_xz=24/105,

M_yz=0.

Следовательно, координаты центра масс данного тела равны:

.