Расчёт локсодромического

и ор­тодромического расстояний.

Локсодромия и ортодромия

Локсодромия это кривая линия на поверхно­сти Земли, пересекающая все меридианы под по­стоянным углом К. Лежащее на постоянном курсе судно перемещается по локсодромии.

Локсодромия является логарифмической спи­ралью, стремящейся к полюсу.

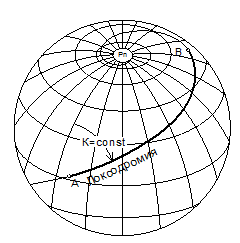
Отрезок локсодромии, заключённый между двумя точками, например А и В, не является кратчайшим расстоянием между ними на по­верхности Земли.

Ортодромия (большой круг) – пересечение по­верхности земного шара и плоскости, проходя­щей через его центр. Отрезок ортодромии, за­ключённый между двумя точками (дуга большого круга - ДБК), является кратчайшим расстоянием между ними на поверхности Земли. Ортодро­мия пересекает меридианы под разными углами, поэтому для перехода по ортодромии необхо­димо постоянно изменять курс.

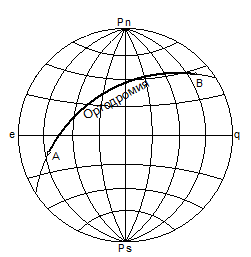
Чем больше разность долгот Δλ между на­чальным и конечным пунктами (точки А и В), тем больше разница между локсодромическим Sлок и ортодромическим Sорт расстояниями. Особенно существенной эта разница может оказаться при трансокеанских переходах. По­этому при выборе маршрута перехода через океан необходимо оценить целесообразность этого перехода по ортодромии.

Критерием целесообразности перехода по ортодромии является относительная разность расстояний:

ΔS = (Sлок – Sорт)/ Sлок·100%;

где Sлок – расстояние по локсодромии;

Sорт - расстояние по ортодромии.

Если ΔS ≥ 0,5%, то переход по ортодромии может быть предпочтительнее.

Расчёт локсодромического расстояния

Для вычисления локсодромического расстояния между двумя точками используется формула аналитического счисления

Sлок = Δφ·secКлок,

где Δφ = φк – φн разность широт начального φн и конечного φк пунктов;

Клок – локсодромический курс между пунктами отхода и прихода, рассчитывается по формуле

tgK = Δλ/ΔD.

Здесь Δλ = λк – λн разность долгот началь­ного λн и конечного λк пунктов.

ΔD - разность меридиональных час­тей этих пунктов, рассчитывается по таблице 2.28а МТ-2000.

Расчёт ортодромического расстояния

Для вычисления ортодромического расстоя­ния применяется формула косинуса стороны из сферической тригонометрии.

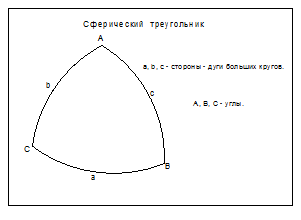Формула косинуса стороны:

cosa = cosb·cosc + sinb·sinc·cosA.

Заменим в этой формуле сторону а длиной ортодромии между пунктами отхода А и при­хода В - Sорт:

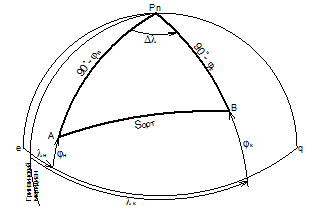В результате получим:

cosSорт = cos(90º- φн)cos(90º- φк)+

+sin(90º- φн)sin(90º- φк)cosΔλ.

где Sорт – ортодромическое расстояние;

90º-φн и 90º-φк – стороны сферического треугольника, отрезки меридианов пунктов от­хода А и прихода В (PnA и PnB);

Δλ = λк-λн - угол сферического треугольника при полюсе Pn, разность долгот между пунк­тами отхода А и прихода В.

Так как cos(90º- α) = sinα, sin(90º- α)= cosα, следовательно:

cosSорт = sinφн·sinφк + cosφн·cosφк·cosΔλ.

Для вычисления Sлок и Sорт вручную использу­ются таблицы десятичных логарифмов чисел и тригонометрических функций.

Расчёт локсодромического

и ортодроми­ческого расстояний

по картам

Ортодромическое расстояние можно рассчи­тать по карте в гномонической проекции. Для этого на карте помещены специальные таблицы, номограмма и указания по их использованию.

Локсодромическое расстояние можно снять по генеральной карте в меркаторской проекции с помощью прокладочного инструмента.