Энтропия. Второй и третий законы термодинамики
Все процессы, протекающие в окружающем нас мире, можно разделить на самопроизвольные (иначе: естественные или положительные) и несамопроизвольные (иначе: неестественные или отрицательные).
Самопроизвольные процессы – это процессы, протекающие без вмешательства со стороны окружающей среды и сопровождающиеся уменьшением внутренней энергии системы и передачей энергии в окружающую среду в форме теплоты или работы. Такие процессы завершаются равновесным состоянием, из которого сама система без сообщения ей энергии извне выйти уже не сможет. Равновесное состояние (термодинамическое равновесие) – это такое термодинамическое состояние системы, когда при постоянных внешних условиях параметры системы (Р, V, Т, состав и т. д.) не изменяются во времени. Примерами самопроизвольных процессов являются:
- расширение газа и заполнение им свободного объёма;
- переход теплоты от горячего тела к холодному;
- диффузия вещества из области большей концентрации в область меньшей концентрации;
- перемещение груза на более низкий уровень;
- любая реакция, используемая в работающем гальваническом элементе;
- сгорание вещества (например, сгорание водорода с образованием воды) и др.
Несамопроизвольные процессы – это процессы, которые не могут совершаться без передачи энергии из окружающей среды в виде теплоты или работы. В изолированной системе (ввиду отсутствия внешнего воздействия) такие процессы протекать не могут. Примерами несамопроизвольных процессов являются:
- сжатие газа до меньшего объёма;
- переход теплоты от холодного тела к горячему;
- диффузия вещества из области меньшей концентрации в область большей концентрации;
- перемещение груза на более высокий уровень;
- зарядка гальванического элемента от внешнего источника тока;
- электролитическое разложение воды на водород и кислород и др.
Один из факторов самопроизвольности процессов, протекающих в открытых и закрытых системах, (в частности – химической реакции) – энергетический фактор. Согласно принципу Бертло –Томсена (предложен независимо друг от друга в 1853 г. Х. Томсеном и в 1867 г. М. Бертло), самопроизвольно могут протекать только реакции, сопровождающиеся выделением теплоты, т. е. экзотермические реакции (DrH < 0).
Действительно, большинство экзотермических химических реакций протекает самопроизвольно, однако есть ряд эндотермических процессов, которые также протекают самопроизвольно. Например, растворение ряда солей (KCl, K2SO4, NH4Cl) в воде. Следовательно, кроме энергетического фактора есть и другая движущая сила самопроизвольного процесса. Эта сила заключается в стремлении частиц системы (молекул, атомом, ионов) к хаотичному движению, а самой системы – к переходу от более упорядоченного состояния к менее упорядоченному.
На рис. 2.2 изображён изолированный сосуд (изолированная система!), разделённый перегородкой на две части, в левой части находится газообразный водород, в правой – газообразный хлор. При разрушении перегородки газы вследствие хаотичного движения их молекулы самопроизвольно смешаются и равномерно распределятся по всему объёма сосуда. Обратный процесс разделения газов самопроизвольно идти не может (вернее, может с ничтожно малой вероятностью). Допустим, в системе находится по 1 моль H2 и Cl2 т. е. по 6,022·1023 молекул каждого газа). Математическая вероятность того, что одна молекула H2 окажется в левой части сосуда равна 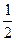 , соответственно, вероятность нахождения одной молекулы Cl2 в правой части сосуда также равна
, соответственно, вероятность нахождения одной молекулы Cl2 в правой части сосуда также равна 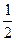 . Следовательно, вероятность того, что в силу своего хаотичного движения все молекулы H2 соберутся в левой части, а все молекулы Cl2 – в правой части равна
. Следовательно, вероятность того, что в силу своего хаотичного движения все молекулы H2 соберутся в левой части, а все молекулы Cl2 – в правой части равна 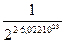 , что составляет ничтожно малую величину.
, что составляет ничтожно малую величину.
Таким образом, система с преобладающей вероятностью самопроизвольно переходит из более упорядоченного состояния (газы разделены) в менее упорядоченное (газы смешаны), т. е. в сторону увеличения беспорядка.

Рис. 2.2.Самопроизвольное смешение газов – переход системы
из более упорядоченного состояния в менее упорядоченное
Для оценки такого стремления системы к менее упорядоченному состоянию было введено понятие «энтропия» (обозначается символом S), т. е. энтропийный фактор самопроизвольности. Функция S была впервые предложена в классической термодинамике в 1865 г. Р. Клаузиусом для определения меры необратимого рассеяния энергии, так как все самопроизвольные процессы должны сопровождаться равномерным распределением (рассеянием) энергии (отсюда ещё одно название самопроизвольных процессов – диссипативные процессы (от лат. dissipatio – рассеяние)). По Клаузиусуэнтропия («эн» для созвучия со словом «энергия», «тропия» от греч. τρόπος – преобразование, что указывает на принцип эквивалентности преобразований, которые претерпевает система в круговом процессе при возвращении к начальному состоянию) – это функция состояния термодинамической системы, изменение которой DS в изотермическом процессе равно приведённой теплоте процесса, т. е. отношению количества теплоты Q, сообщённой системе или отведённой от неё к термодинамической температуре T:
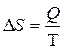 . .
| (2.24) |
В статистической термодинамике существует другое определение: энтропия – это мера беспорядка системы. Энтропия измеряется в тех же единицах, что и теплоёмкость: 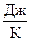 ,
, 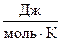 (мольная энтропия),
(мольная энтропия), 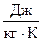 (удельная энтропия).
(удельная энтропия).
Если с понятием «энергия» связан первый закон термодинамики, то с понятием «энтропия» связан второй закон термодинамики. Второй закон даёт ответы на вопросы:
- При каких условиях (Р, V, Т, состав и т. д.) в системе будет протекать самопроизвольный процесс?
- При каких условиях в системе установится состояние равновесия?
- Как те или иные воздействия на систему влияют на состояние равновесия?
Существует множество формулировок второго закона, предложенных во 2-ой половине XIX века рядом учёных: Р. Клаузиусом, У. Томсоном (Кельвином), Л.Э. Больцманом, В. Оствальдом и др. Эти формулировки сводятся к одной общей идее, позволяющей трактовать второй закон, как закон возрастания энтропии:
В любой изолированной системе самопроизвольные процессы протекают с возрастанием энтропии (DS > 0). В состоянии равновесия энтропия достигает максимального значения, а её изменение равно нулю (DS = 0).
Таким образом, для изолированной системы критерий самопроизвольности процесса – увеличение энтропии (DS > 0), а критерий несамопроизвольности – уменьшение энтропии (DS < 0) (см. рис. 2.2).
В отличие от других функций состояния (например, U и H) можно определить не только изменение, но и абсолютное значение энтропии. Абсолютная энтропия S связана с термодинамической вероятностью системы. Термодинамическая вероятность w– это число способов, которыми частицы (молекулы, атомы, электроны и т. д.), составляющие систему, можно распределить по доступным для них уровням энергии при заданном объёме и внутренней энергии системы. Связь между w и S выражается формулой Больцмана-Планка (впервые в качестве гипотезы была предложена Л.Э. Больцманом в 1872 г., а в 1879 г. подтверждена М. Планком):
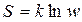 , ,
| (2.25) |
где k = 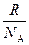 – постоянная Больцмана,
– постоянная Больцмана, 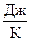 (1,38×10–23).
(1,38×10–23).
Рассмотрим какой-либо идеальный (т. е. без дефектов) кристалл – например, CsF(кр.). Ионы Cs+ и F–, расположенные в узлах кристаллической решётки, совершают температурные колебания около равновесных положений. По мере снижения температуры энергия колебаний ионов уменьшается, соответственно снижается термодинамическая вероятность кристалла w. Наконец, при условии абсолютного нуля (T = 0 K) можно обнаружить, что ионы «вмёрзли» в узлы решётки, т. е. вариации состояния кристалла исключены и w = 1. Согласно формуле Больцмана-Планка (2.25) в этом случае S = 0. Отсюда вытекает постулат Планка (впервые сформулирован М. Планком в 1911 г.):
Энтропия любого термодинамически равновесного вещества (например, идеального кристалла) при абсолютном нуле температуры равна нулю.
Постулат Планка – это одна из формулировок третьего закона термодинамики. Третий закон уступает по своей фундаментальности первому и второму законам термодинамики и часто рассматривается, как дополнение второго закона.
По мере увеличения температуры T вещества растёт скорость различных видов движений частиц, т. е. термодинамическая вероятность системы w. Соответственно растёт и энтропия S вещества (рис. 2.3). При температуре плавления Tm происходит переход вещества из твёрдого состояния в жидкое – значительно увеличивается беспорядок системы, энтропия скачкообразно возрастает на величину энтропии плавления DmS. Особенно резко энтропия возрастает при фазовом переходе из жидкого состояния в газообразное (энтропия испарения DvS при температуре испарения Tv). Из всех агрегатных состояний вещества газ обладает наибольшей энтропией, т. к. частицы газа наименее упорядочены. Газы называют носителями энтропии (сам термин «газ» возник от греч. χάος – хаос, беспорядок). Зная, что энтропия увеличивается с увеличением беспорядка системы (при плавлении, испарении, увеличении количества газов и т. д.), можно определить знак DS, не производя расчётов. Например:
H2O(кр.) ® H2O(ж.), DS > 0;
H2O(г.) ® H2O(ж.), DS < 0;
3O2(г.) ® 2O3(г.), DS < 0;
CaCO3(кр.) ® CaO(кр.) + CO2(г.), DS > 0;
H2(г.) + Cl2(г.) ® 2HCl(г.), DS » 0.
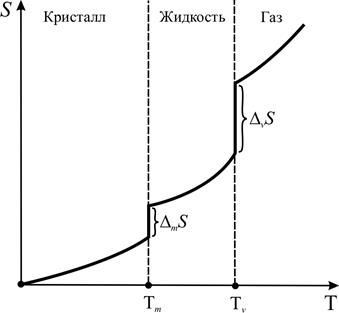
| Рис. 2.3.Схема изменения энтропии вещества S с увеличением температуры T |
Фазовые переходы первого рода при постоянном давлении происходят изотермически (т. е. – при постоянной температуре фазового перехода Ttr). Поэтому изменение энтропии при фазовом превращении (т. е. энтропию фазового перехода DtrS) можно рассчитать непосредственно из уравнения (2.24), учитывая, что Q является теплотой фазового перехода DtrН:
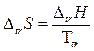 . .
| (2.26) |
Пример 2.8. Рассчитайте для воды стандартную энтропию плавления DmS° при температуре плавления Тm = 273,15 К и стандартную энтропию испарения DvS° при температуре испарения Тv = 373,15К.
Решение:
По справочнику [Справочник химика Т1, Волков] находим стандартные теплоты плавления и испарения воды при данных температурах плавления и испарения соответственно:
при Тm = 273,15 К стандартная теплота плавления DmН°(H2O) = 6,01 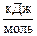 ;
;
при Тv = 373,15 К стандартная теплота испарения DvН°(H2O) = 40,66 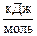 .
.
По формуле (2.26) рассчитаем DmS° и DvS° воды:
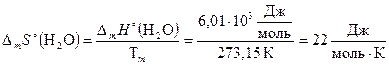 ;
;
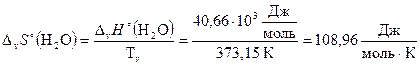 .
.
Ответ: DmS°(H2O) = 22 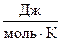 ; DvS°(H2O) = 108,96
; DvS°(H2O) = 108,96 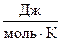 .
.
Зная абсолютные энтропии всех веществ, участвующих в реакции, можно рассчитать изменение энтропии химической реакции DrS. При температуре Т DrST рассчитывают, как разность сумм абсолютных энтропий ST продуктов реакции и исходных веществ, взятых с коэффициентами, равными стехиометрическим (аналогично расчёту теплового эффекта реакции DrНT по первому следствию из закона Гесса – см. § 2.3). Для произвольной изобарно-изотермической реакции вида (2.19) при стандартных состояниях веществ DrS°T рассчитывают по формуле:
| DrS°T = [cS°T(C) + dS°T(D)] – [aS°T(A) + bS°T(B)] | (2.27) |
или, в общем случае:
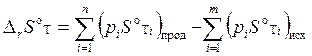 , ,
| (2.28) |
где S°T – абсолютные энтропии продуктов реакции и исходных веществ в стандартных состояниях при постоянном давлении и данной температуре.
В справочниках значения S°T приводятся для Т = 298,15 К (обозначаются S°298).
Пример 2.9. Рассчитайте изменение энтропии реакции при Т = 298,15 К и Р = 1 атм DrS°298, пользуясь данными по абсолютным стандартным энтропиям веществ – участников реакции S°298:
CaC2(a-кр.) + 2H2O(ж.) ® Ca(OH)2(кр.) + C2H2(г.).
Решение:
Абсолютные стандартные энтропии веществ – участников реакции S°298 [Равдель]:
| Вещество | CaC2(a-кр.) | H2O(ж.) | Ca(OH)2(кр.) | C2H2(г.) |
S°298, 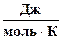
| 69,96 | 69,95 | 83,39 | 200,82 |
Рассчитаем DrS°298 по формуле (2.27):
DrS°298 = [S°298(Ca(OH)2(кр.)) + S°298(C2H2(г.))] – [S°298(CaC2(a-кр.)) + 2S°298(H2O(ж.))] =
= [83,39 + 200,82] – [69,96 + 2×(69,95)] = 74,35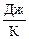 .
.
Так как в данной реакции возрастает количество газообразных веществ (т. е. возрастает беспорядок), энтропия системы увеличивается (DrS°298 > 0).
Ответ: DrS°298 = 74,35 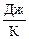 .
.
Энергия Гиббса
Согласно второму закону термодинамики, для изолированной системы энтропия S – это критерий, который характеризует возможность, направление и предел самопроизвольного протекания термодинамических процессов (DS > 0 – в системе протекает самопроизвольный процесс, DS = 0 – система находится в состоянии равновесия, см. § 2.4). Однако, на практике рассматривают не идеальные изолированные, а реальные закрытые или открытые системы. В частности, в химической технологии процессы протекают либо в открытых аппаратах (при постоянных P и T), либо в закрытых аппаратах, например в автоклавах (при постоянных V и T). В таких процессах самопроизвольные процессы могут сопровождаться уменьшением энтропии системы. Никакого противоречия со вторым законом термодинамики тут нет, так как в закрытых и открытых системах на энтропийный фактор самопроизвольности накладывается энергетический фактор – происходит обмен теплотой и работой с окружающей средой (в открытых – ещё и обмен веществом). Благодаря этому, система при уменьшении собственной энтропии Sсист может увеличить энтропию окружающей среды Sокр. Энтропия Вселенной SВсел = Sсист + Sокр в итоге увеличится.
Поэтому для того, чтобы в простой форме определить направление процесса и условия термодинамического равновесия системы в качестве критерия необходимо использовать не S, а какие-то другие термодинамические функции. Одной из таких функций является энергия Гиббса G, предложенная Д.У. Гиббсом в 1874 г. Рассмотрим смысл этой функции.
Если в системе совершается не только работа против внешнего давления PDV, но и какая-либо полезная работа W¢ (например, работа электрического тока в гальваническом элементе), то выражение первого закона термодинамики (2.4) примет вид:
| DU = Q – PDV – W¢. | (2.29) |
Выразив отсюда полезную работу, получим:
| W¢ = Q – PDV – DU. | (2.30) |
Учитывая уравнение (2.24), получим:
| W¢ = TDS – PDV – DU. | (2.31) |
Для изобарно-изотермического процесса (P = const, T = const), уравнение (2.31) примет вид:
| W¢P,T = –D(U + PV – TS)P,T = –D(H – TS)P,T. | (2.32) |
Выражение (функция состояния), стоящее в формуле (2.32) в скобках, и есть энергия Гиббса G:
| G = H – TS. | (2.33) |
Тогда уравнение (2.32) можно записать:
| W¢P,T = –DGP,T. | (2.34) |
P и T являются парой естественных переменных энергии Гиббса, второе её название – изобарно-изотермический потенциал. Если уравнение (2.33) переписать в виде H = G + TS, то энтальпию можно рассмотреть, как состоящую из двух частей: свободной энтальпии G (третье название энергии Гиббса) и связанной энтальпии TS. В изобарно-изотермическом процессе свободная энтальпия превращается в полезную работу (в соответствие с уравнением (2.34)), а связанная энтальпия переходит в теплоту.
На основании вышеизложенного дадим следующее определение. Энергия Гиббса G (изобарно-изотермический потенциал,свободная энтальпия) – это функция состояния, имеющая в качестве естественных переменных давление P и температуру T и определяемая через энтальпию H, энтропию S и температуру T равенством G = H – TS. В изобарно-изотермическом процессе убыль энергии Гиббса для данной системы равна максимальной полезной работе, производимой системой.
Так как абсолютную величину энтальпии H измерить невозможно (см. § 2.1), также невозможно измерить и абсолютную величину энергии Гиббса G. На практике определяют изменение DG = G2 – G1, которые считаются положительными, если G системы в рассматриваемом процессе возрастает (часто слово «изменение» опускают, тогда параметр DG называют просто «энергия Гиббса»). В изобарно-изотермическом процессе DGP,T рассчитывают по формуле:
| DGP,T = DHP,T – TDSP,T. | (2.35) |
Энергия Гиббса в СИ выражаются в Дж. В термодинамических расчётах используют удельную ( 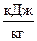 ) и мольную(
) и мольную( 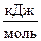 )DG.
)DG.
Итак, большинство химических реакций протекает в открытых системах (при постоянных P и T), поэтому критерием их самопроизвольности является энергия Гиббса DGP,T, включающая в себя энергетический фактор DHP,T и энтропийный фактор DST. Учитывая, что согласно принципу Бертло – Томсена реакции протекают самопроизвольно при DHP,T < 0, а согласно второму закону термодинамики – при DST > 0, то очевидно, что в открытых системах:
- реакции могут протекать самопроизвольно (т. е. могут протекать прямые реакции) при DGP,T < 0;
- реакции не могут протекать самопроизвольно (т. е. могут протекать обратные реакции) при DGP,T> 0;
- устанавливается термодинамическое равновесие при DGP,T= 0.
Для большинства химических реакций при относительно низких температурах (T примерно < 1000 K) определяющим в знаке DGP,T является энергетический фактор (çDHP,Tç > çTDSTç), а при относительно высоких (T примерно ³ 1000 K) – энтропийный фактор (çDHP,Tç < çTDSTç). Если в ходе реакции DST » 0, температура на направление реакции практически не влияет. Для оценки направления протекания химической реакции или для предсказания термодинамической возможности её протекания в данном направлении используют стандартную энергию Гиббса реакции DrG°T. DrG°T можно рассчитать, зная стандартные энергии Гиббса образования всех веществ, участвующих в реакции.
Стандартная энергия Гиббса образования DfG°T – это энергия Гиббса образования 1 моль данного соединения из простых веществ, отвечающих наиболее устойчивому состоянию рассматриваемого элемента при данной температуре и атмосферном давлении (101325 Па). В справочниках значения DfG°T приводятся для Т = 298,15 К (обозначаются DfG°298). Например: энергия Гиббса образования 1 моль сульфита натрия Na2SO3:
2Na(кр.) + S(ромб.) + 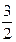 О2(г.) ® Na2SО3(кр.), О2(г.) ® Na2SО3(кр.),
| DfG°298(Na2SО3(кр.)) = –1001,21 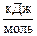 . .
|
Стандартные энергии Гиббса образования простых веществ в термодинамически устойчивом состоянии принимаются равными нулю (например: DfG°298(H2(г.)) = 0).
Аналогично расчёту теплового эффекта реакции по 1-му следствию из закона Гесса (см. § 2.3) для произвольной изобарно-изотермической реакции вида (2.19) DrG°T рассчитывают по формуле:
| DrG°T = [cDfG°T(C) + dDfG°T(D)] – [aDfG°T(A) + bDfG°T(B)] | (2.36) |
или, в общем случае:
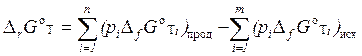 , ,
| (2.37) |
Кроме того, для расчёта DrG°T применяют уравнение (2.35) в форме:
| DrG°T = DrH°T – TDrS°T. | (2.38) |
Пример 2.10. Рассчитайте энергию Гиббса DrG°T реакции термического разложения кристаллического карбоната кальция CaCO3 при температурах 25 и 1500 °С, если DrH°T = 178,1 кДж, DrS°T = 165,7 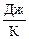 . Выше какой температуры данная реакция для стандартного состояния веществ может протекать самопроизвольно? Зависимостью DrH°T и DrS°T от температуры пренебречь.
. Выше какой температуры данная реакция для стандартного состояния веществ может протекать самопроизвольно? Зависимостью DrH°T и DrS°T от температуры пренебречь.
Решение:
CaCO3(кр.) 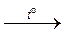 CaO(кр.) + CO2(г.).
CaO(кр.) + CO2(г.).
1. DrG°T при температуре 25 °С (298,15 К) DrG°298 рассчитаем по формуле (2.37).
Стандартные энергии Гиббса образования веществ – участников реакции DfG°298
[Равдель]:
| Вещество | CaCO3(кр.) | CaO(кр.) | CO2(г.) |
DfG°298, 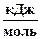
| –1128,35 | –603,46 | –394,37 |
DrG°298 = [DfG°298(CaO(кр.)) + DfG°298(CO2(г.))] – DfG°298(CaCO3(кр.)) =
= [–603,46 + (–394,37)] – (–1128,35) = 130,5 кДж.
DrG°298 > 0 – при Т = 298,15 К данная реакция не может протекать самопроизвольно.
2. DrG°T при температуре 1500 °С (1773,15 К) DrG°1773 рассчитаем по формуле (2.38):
DrG°1773 = DrH°T – 1773,15·DrS°T = 178,1 кДж – 1773,15´165,7×10–3 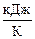 = –115,7 кДж.
= –115,7 кДж.
DrG°1773 < 0 – при Т = 1773,15 К данная реакция может протекать самопроизвольно.
3. Рассчитаем температуру Т, выше которой реакция может протекать самопроизвольно.
В состоянии термодинамического равновесия DrG°T = 0.
Тогда из уравнения (2.38) DrH°T = TDrS°T,
отсюда 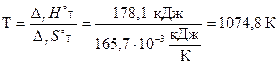 .
.
Ответ: DrG°298 = 130,5 кДж; DrG°1773 = –115,7 кДж;
реакция может протекать самопроизвольно при Т > 1074,8 К.
Дата добавления: 2016-06-29; просмотров: 4423;










