Закон сохранения электрического заряда

Существует два типа зарядов – положительные и отрицательные; одноименные заряды друг от друга отталкиваются, разноименные – притягиваются. При электризации трением всегда заряжаются оба тела, причем равными по величине но разноименными зарядами.

Опытным путем американский физик Р.Милликен (1868–1953) и советский физик А.Ф.Иоффе доказали, что электрический заряд дискретен, т. е. заряд любого тела составляет целое кратное от некоторого элементарного электрического заряда е (е = 1,6.10^-19Кл). Электрон (m_e = 9,11.10^{-31 кг) и протон (m}_p = 1,67.10^{-27 кг) являются соответственно носителями элементарных отрицательного и положительного зарядов.}

Из обобщения опытных данных был установлен фундаментальный закон природы, впервые сформулированный английским физиком М.Фарадеем (1791 – 1867), – закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы.

Электрический заряд – величина релятивистски инвариантная, т. е. не зависит от системы отсчета, а значит, не зависит от того, движется этот заряд или покоится.

Наличие носителей заряда (электронов, ионов) является условием того, что тело проводит электрический ток. В зависимости от способности тел проводить электрический ток они делятся на проводники, диэлектрики и полупроводники Проводники – тела, в которых электрический заряд может перемещаться по всему его объему. Проводники делятся на две группы: 1) проводники первого рода (например, металлы) – перенесение в них зарядов (свободных электронов) не сопровождается химическими превращениями; 2) проводники второго рода (например, расплавленные соли, растворы кислот) – перенесение в них зарядов (положительных и отрицательных ионов) ведет к химическим изменениям. Диэлектрики (например, стекло, пластмассы) – тела, которые не проводят электрического тока; если к этим телам не прикладывается внешнее электрическое поле, в них практически отсутствуют свободные носители заряда. Полупроводники (например, германий, кремний) занимают промежуточное положение между проводниками и диэлектриками, причем их проводимость сильно зависит от внешних условий, например температуры.

Единица электрического заряда (производная единица, так как определяется через единицу силы тока) – кулон (Кл) – электрический заряд проходящий через поперечное сечение при токе силой 1 А за время 1 с.

2.Закон Кулона

Закон взаимодействия неподвижных точечных электрических зарядов установлен в 1785 г. Ш.Кулоном с помощью крутильных весов (ранее этот закон был открыт Г. Кавендишем, однако его работа оставалась неизвестной более 100 лет). Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

Закон Кулона: сила взаимодействия F между двумя точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q₁, и Q₂ и обратно пропорциональна квадрату расстояния r между ними:

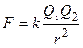, (1)

где k – коэффициент пропорциональности, зависящий от выбора системы единиц.

Кулоновская сила F направлена вдоль прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F< 0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов.

В векторной форме закон Кулона имеет вид

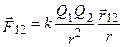(.2)

где F₁₂, – сила, действующая на заряд Q₁ со стороны заряда Q₂, r₁₂ – радиус вектор, соединяющий заряд Q₁ с зарядом Q₂.

Если взаимодействующие заряды находятся в однородной и изотропной среде, то сила взаимодействия 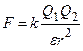, где ε – безразмерная величина – диэлектрическая проницаемость среды, показывающая, во сколько раз сила F взаимодействия между зарядами в данной среде меньше их силы F_о взаимодействия в вакууме: ε =F_о/F. Для вакуума ε = 1.

В СИ коэффициент пропорциональности принимается равным .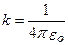

Тогда закон Кулона запишется в окончательном виде: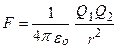

Величина ε_о называется электрической постоянной; она относится к числу фундаментальных физических постоянных и равна ε_о = 8,85.10^-12 Кл /(Н м ). Тогда k = 9.10⁹ м/Ф.

3.Электростатическое поле и его напряженность

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит в пространстве, окружающем электрические заряды, существует силовое поле. Согласно представлениям современной физики, поле реально существует и наряду с веществом является одним из видов материи, посредством которого осуществляются определенные взаимодействия между макроскопическими телами или частицами, входящими в состав вещества. В данном случае говорят об электрическом поле – поле, посредством которого взаимодействуют электрические заряды. Мы будем рас сматривать электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими.

Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд – такой заряд, который своим действием не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q_о, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона, пропорциональна пробному заряду Q_о. Поэтому отношение F/Q_o не зависит от пробного заряда и характеризует электрическое поле в той точке, где пробный заряд находится. Эта величина является силовой характеристикой электростатического поля и называется напряженностью.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд помещенный в эту точку поля: E=F/Q_o.

Направление вектора Е совпадает с на правлением силы, действующей на положительный заряд. Единица напряженности электростатического поля – ньютон на кулон (Н/Кл): 1 Н/Кл – напряженность такого поля, которое на точечный заряд 1 Кл действует силой в 1 Н. 1 Н/Кл = 1 В/м, где В (вольт) – единица потенциала электростатического поля (см. 84).

Напряженность поля точечного заряда (для ε = 1)

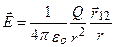(3)

или в скалярной форме

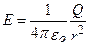
Вектор Е во всех точках поля направлен радиально от заряда, если он положителен и радиально к заряду, если отрицателен.

Графически электростатическое поле изображают с помощью линий напряженности (силовых линий), которые проводят так, чтобы касательные к ним каждой точке пространства совпадали по направлению с вектором напряженности в данной точке поля. Так как в каждой данной точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности – радиальные прямые, выходящие из заряда, если он положителен, и входящие в него, если заряд отрицателен. Вследствие большой наглядности графический способ представления электрического поля широко применяется в электротехнике.

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и величину напряженности электростатического поля, условились проводить их с определенной густотой: число линий напряженности, пронизывающих единицу поверхности, перпендикулярной линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль к которой образует угол α с вектором Е, равно ЕdS cos α. Величина dФ_E = ЕdS называется потоком вектора напряженности через площадку dS. Здесь dS = dS n– вектор, модуль которого равен dS, а направление совпадает с нормалью n к площадке. Выбор направления вектора n (а, следовательно, и dS) условен, так как его можно направить в любую сторону.

Для произвольной замкнутой поверхности S поток вектора Е через эту поверхность

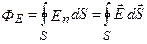
где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охватываемой поверхностью.

В истории развития физики имела место борьба двух теорий – дальнодействия и близкодействия. В теории дальнодействия принимается, что электрические явления определяются мгновенным взаимодействием зарядов на любых расстояниях. Согласно теории близкодействия, все электрические явления определяются изменениями полей зарядов, причем эти изменения распространяются в пространстве от точки к точке с конечной скоростью. Применительно к электростатическим полям обе теории дают одинаковые результаты, хорошо согласующиеся с опытом. Переход же к явлениям, обусловленным движением электрических зарядов, приводит к несостоятельности теории дальнодействия, поэтому современной теорией взаимодействия заряженных частиц является теория близкодействия.

4.Принцип суперпозиции электростатических полей. Поле диполя

Рассмотрим метод определения величины и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой не подвижных зарядов Q₁, Q₂, … Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил, т. е. результирующая сила F, действующая со стороны поля на пробный заряд Q_о равна векторной сумме сил F_i, приложенных к нему со стороны каждого из зарядов Q_i: 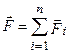.Так как F = Q_oE и F_i = Q_oE_{i ,}–где Е напряженность результирующего поля, а Е_i; – напряженность поля, создаваемого зарядом Q_i;. Подставляя, получим 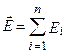.Эта формула выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рас считать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Применим принцип суперпозиции для расчета электростатического поля электрического диполя. Электрический диполь – система двух равных по модулю разноименных точечных зарядов (+Q, –Q), расстояние 1 между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя. Вектор p = |Q|l совпадающий по направлению с плечом диполя и равный произведению заряда Q на плечо 1, называется электрическим моментом диполя р или дипольным моментом

Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке

Е= Е₊ + Е_- , где Е₊ и Е_- – напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряженность поля на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолжении оси диполя в точке А. Как видно из рисунка, напряженность поля диполя в точке А направлена по оси диполя и по модулю равна Е= Е₊ - Е_-

Обозначив расстояние от точки А до середины оси диполя через r, определим напряженности полей, создаваемых зарядами диполя и сложим их

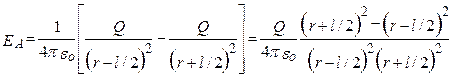
Согласно определению диполя, l/2 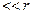, поэтому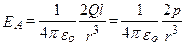

2.Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке В. Точка В равноудалена от зарядов, поэтому

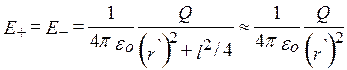(4),

где r' – расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е_B, получим

,

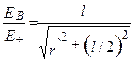откуда E_B= E₊l /r. (5)

Подставив в выражение (5) значение (4), получим

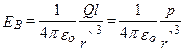
Вектор Е_В имеет направление, противоположное электрическому моменту диполя.

5.Теорема Гаусса для электростатического поля в вакууме

Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К.Гауссом (1777 – 1855) теорему, определяющую поток вектора напряженности электрического поля через произвольную замкнутую поверхность.

Известно, поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре, равен

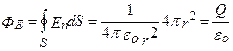
Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд, то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линия напряженности выходит из поверхности, и отрицательным для линии, входящей в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/e_o т. е.

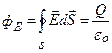
Рассмотрим общий случай произвольной поверхности, окружающей n зарядов. В соответствии с принципом суперпозиции напряженность Е_i поля, создаваемого всеми зарядами, равна сумме напряженностей, создаваемых каждым зарядом в отдельности E = SE_i. Поэтому

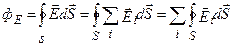
Каждый из интегралов, стоящий под знаком суммы равен Q_i / e_o. Следовательно,

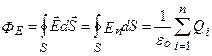(5А)

Эта формула выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε_о. Эта теорема выведена математически для векторного поля любой природы русским математиком М.В.Остроградским (1801–1862), а затем независимо от него применительно к электростатическому полю – К.Гауссом.

В общем случае электрические заряды могут быть «размазаны» с некоторой объемной плотностью ρ = dQ/dV, различной в разных местах пространства. Тогда суммарный заряд заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V равен .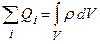

Тогда теорему Гаусса можно записать так:

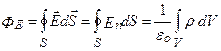
6. Применение теоремы Гаусса к

расчету некоторых электростатических полей в вакууме

1.Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS – заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности выделим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosα = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Е_n совпадает с Е), т. е. равен 2ЕS. Заряд, заключенный внутри цилиндра, равен σS. Согласно теореме Гаусса 2ЕS = σS /ε_o, откуда

E = σ /2ε_o (6)

Из формулы вытекает, что Е не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

2.Поле двух бесконечных параллельных разноименно заряженных плоскостей. Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +σ и –σ. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Как видно из рисунка, слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля Е =0. В области между плоскостями Е = Е₊+ Е_– (Е₊ и Е_– определяются по формуле (6), поэтому результирующая напряженность Е = σ/ε_о. Таким образом, поле в данном случае сосредоточено между плоскостями и является в этой области однородным.

3.Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +σ. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально). Выделим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса, 4πr²E = Q/ε_o, откуда

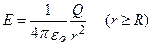(7)

Если r'<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е=0). Вне этой поверхности поле убывает с расстоянием r по такому же закону, как у точечного заряда.

4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ = dQ/dV– –заряд приходящийся на единицу объема). Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае. Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q' =4/3 πr'³ρ. Поэтому, согласно теореме Гаусса, 4πr'²Е = Q'/ε_о = =4/3 πr'³ρ/ε_о. Учитывая, что ρ = Q/(4/3πR³), получим

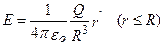. (8)

Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (7), а внутри его изменяется линейно с расстоянием r' согласно выражению (8).

5.Поле равномерно заряженного бесконечного цилиндра. Бесконечный цилиндр радиуса R заряжен равномерно с линейной плотностью τ (τ = dQ/dl– – заряд приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут радиальными прямыми, перпендикулярными поверхности цилиндра. В качестве замкнутой поверхности выделим коаксиальный с заряженным цилиндр радиуса r и длиной l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность 2πrlE.

По теореме Гаусса, при r >R 2πrlE = τl/ε_o, откуда

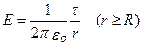(9)

Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (8), внутри же его поле отсутствует.

7.Циркуляция вектора напряженности электростатического поля

Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд Q_o, то сила, приложенная к заряду, совершает работу. Работа на элементарном пути dl равна .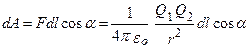

Так как dl cos α = dr, то 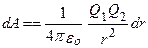. Работа при перемещении заряда Q_o из точки 1 в точку 2

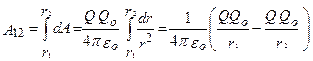(10)

не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Из формулы (10) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L равна нулю, т. е.

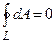(11)

Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд то элементарная работа сил поля на пути dl равна Edl = Е_ldl, где Е_l = Еcosα – проекция вектора Е на направление элементарного перемещения. Тогда формулу можно записать в виде 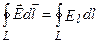= 0.

Интеграл 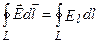называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Из этого следует также, что линии напряженности электростатического поля не могут быть замкнутыми.

Полученная формула справедлива только для электростатического поля. В дальнейшем будет показано, что поле движущихся зарядов потенциальным не является и условие (5*) для него не выполняется.

7.Потенциал электростатического поля

Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа. Как известно из механики, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q_o в начальной и конечной точках поля заряда Q: ,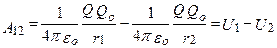

откуда следует, что потенциальная энергия заряда Q_o в поле заряда Q равна 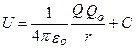, которая, как и в механике, определяется с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r→ ∞) потенциальная энергия обращается в нуль (U = 0), то С = 0 и потенциальная энергия заряда Q_o, находящегося в поле заряда Q на расстоянии г от него, равна

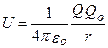(12)

Для одноименных зарядов Q_oQ> 0 и потенциальная энергия их взаимодействия (отталкивания) положительна. Для разноименных зарядов Q_oQ <0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.

Если поле создается системой n точечных зарядов Q₁, Q₂, …Q_n, то при соблюдении принципа суперпозиции потенциальная энергия U заряда Q_o находящегося в этом поле, равна сумме его потенциальных энергий U_i, создаваемых каждым из зарядов в отдельности

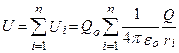(13)

Из формул (12) и (13) вытекает, что отношение U/Q_o не зависит от Q_o и является поэтому энергетической характеристикой электростатического поля, называемой потенциалом:

Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из формул (12) и (13) следует, что потенциал поля, создаваемого точечным зарядом Q, равен

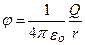(14)

Работа, совершаемая силами электростатического поля при перемещении заряда Q_o из точки 1 в точку 2, может быть представлена как

A₁₂ =U₁-U₂=Q_o(φ₁-φ₂), (15)

т.е. работа равна произведению переносимого заряда на разность потенциалов в начальной и конечной точках.

Работа сил поля при перемещении заряда Q_o из точки 1 в точку 2 может быть записана также в виде

.

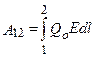Приравняв (14) и (15), придем к соотношению φ₁-φ₂ = 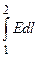, где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.

Если перемещать заряд Q_o из произвольной точки за пределы поля, т.е. в бесконечность, где по условию потенциал равен нулю, то работа сил электростатического поля, согласно (15), A_∞=Q_oφ или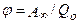

Таким образом, потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Из выражения (14) следует, что единица потенциала – вольт (В): 1 В – есть потенциал такой точки поля, в которой снаряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта можно показать, что введенная ранее единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл = 1 Н м/(Кл м) = 1 Дж/(Кл м) = 1 В/м.

Из формул (14) и (15) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы снарядов равен алгебраической сумме потенциалов полей всех этих зарядов. В этом заключается существенное преимущество скалярной энергетической характеристики электростатического поля – потенциала – перед его векторной силовой характеристикой – напряженностью, которая равна геометрической сумме напряженностей слагаемых полей.

Напряженность как градиент потенциала. Эквипотенциальные поверхности

Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом – энергетической характеристикой поля.

Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и х₂ – х₁ = dx, равна Е_xdx. Та же работа равна φ₁ – φ₂ = –dφ. Приравняв оба выражения, можем записать 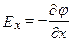, где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей у и z, можем найти вектор Е:

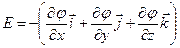, (16)

где i, j, k – единичные векторы координатных осей х, у, z.

Из определения градиента и (1.6) следует, что 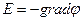, или 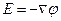, т.е. напряженностьЕполя равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения, пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал φ имеет одно и то же значение.

Таким образом, эквипотенциальные поверхности в данном случае – концентрические сферы. С другой стороны, линии напряженности в случае точечного заряда – радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.

Рассуждения приводят к выводу о том, что линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Е всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим поверхностям.

Эквипотенциальных поверхностей вокруг каждой системы зарядов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.

Зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно определить в каждой точке поля величину и направление напряженности поля. На рисунке для примера показан вид линий напряженности (пунктирные линии) и эквипотенциальных поверхностей (сплошные линии) поля заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом – впадину.

Вычисление потенциала по напряженности поля

Установленная связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.

1.Поле равномерно заряженной бесконечной плоскости определяется формулой Е = σ/2ε_о, где σ – поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х₁ и х₂ от плоскости (используем формулу (16)), равна

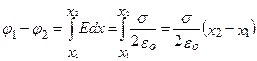
2.Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой Е = σ/ε_о, где σ – поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно d (см. формулу (15)), равна

.

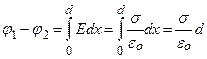3.Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы (r > Q) вычисляется по формуле: 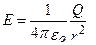. Разность потенциалов между двумя точками, лежащими на расстояниях r₁, и r₂ от центра сферы (r₁>R, r₂>R), равна

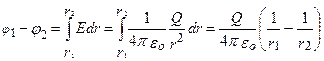
Если принять r₁= R, и r₂ = ∞, то потенциал заряженной сферической поверхности .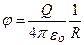

4. Поле равномерно заряженного шара радиуса R с общим зарядом Q вне шара (r>R) вычисляется по формуле (82.3), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r₁, и r₂, от центра шара (r₁>R, r₂>R), определяется формулой (86.2). В любой точке, лежащей внутри шара на расстоянии r' от его центра (r' <R), напряженность определяется выражением (82.4): 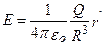.Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁', и r₂′ от центра шара (r₁'<R, r₂′<R), равна

.

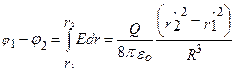5. Поле равномерно заряженного бесконечного цилиндра радиуса R, заряженного с линейной плотностью τ, вне цилиндра (r>R) определяется формулой (15): .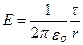

Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁, и r₂, от оси заряженного цилиндра (г₁>R, г₂>R), равна

.

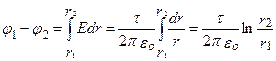Типы диэлектриков. Поляризация диэлектриков

Диэлектрик (как и всякое вещество) состоит из атомов и молекул. Положительный заряд сосредоточен в ядрах атомов, а отрицательный – в электронных оболочках атомов и молекул. Так как положительный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекулы через суммарный заряд +Q, находящийся в центре «тяжести» положительных зарядов, а заряд всех электронов – суммарным отрицательным снарядом –Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом, определенным формулой (80.3).

Первую группу диэлектриков (N₂, H₂ О₂, СН₄..) составляют вещества, молекулы которых имеют симметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю. Молекулы таких диэлектриков называются неполярнымц Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля) и молекула при обретает дипольный момент.

Вторую группу диэлектриков (Н₂О, NН₃, SО₂, СО, и т.д.) составляют вещества, молекулы которых имеют асимметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом. Молекулы таких диэлектриков называются полярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля.

Третью группу диэлектриков (NаС1, КСl, КВг,...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух в