Вероятность появления хотя бы одного события.
ТеоремаВероятность появления хотя бы одного из попарно независимых событий А1, А2,…, Ап равна р (А) = 1 – q1q2…qn , где qi – вероятность события 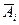 , противоположного событию Аi .
, противоположного событию Аi .
Пример. Сколько нужно произвести бросков монеты, чтобы с вероятностью не менее 0,9 выпал хотя бы один герб?
Решение. Вероятность выпадения герба при одном броске равна вероятности противопо-ложного события (выпадения цифры) и равна 0,5. Тогда вероятность выпадения хотя бы одного герба при п выстрелах равна 1- (0,5)п . Тогда из решения неравенства 1- (0,5)п > 0,9
следует, что п > log210 ≥ 4.
Аксиомы вероятностей.
Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P(A)=m1/n, P(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,
Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P(A), P(B) и P(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B)
Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом.
Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию Р(А)=m/n .
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей: P(A+B)=P(A)+P(B)
Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то
Событием, противоположным событию A, называется событие 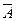 , состоящее в ненаступлении события A. Очевидно, события A и
, состоящее в ненаступлении события A. Очевидно, события A и 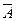 несовместны.
несовместны.
Пусть, например, событие A состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие заключается в том, что изделие стандарту не удовлетворяет. Пусть событие A — выпадение четного числа очков при однократном бросании игральной кости; тогда 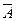 — выпадение нечетного числа очков.
— выпадение нечетного числа очков.
Теорема 1. Для любого события A вероятность противоположного события Р( 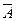 ) = 1- Р(А) выражается равенством
) = 1- Р(А) выражается равенством
Теорема 2. Вероятность невозможного события равна нулю.
Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.
Классическое определение вероятности.
Как было сказано выше, при большом числе n испытаний частота P(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A.
Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).
Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.
Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.
Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них.
Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.
Очевидно, любое событие A и противоположное ему событие 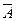 образуют полную группу.
образуют полную группу.
Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.
Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A.
Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению.
Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.
Рассмотрим следующий пример. Пусть брошены две монеты. Найдем вероятность появления двух гербов. Мы имеем 4 равновероятных попарно несовместных исхода, образующих полную группу:
| 1-я монета | 2-я монета | |
| 1-й исход | герб | герб |
| 2-й исход | герб | надпись |
| 3-й исход | надпись | герб |
| 4-й исход | надпись | надпись |
Таким образом, P(герб,герб)=1/4.
Пусть теперь нам стало известно, что на первой монете выпал герб. Как изменится после этого вероятность того, что герб появится на обеих монетах? Так как на первой монете выпал герб, то теперь полная группа состоит из двух равновероятных несовместных исходов:
| 1-я монета | 2-я монета | |
| 1-й исход | герб | герб |
| 2-й исход | герб | надпись |
При этом только один из исходов благоприятствует событию (герб, герб). Поэтому при сделанных предположениях Р(герб,герб)=1/2. Обозначим через А появление двух гербов, а через В — появление герба на первой монете. Мы видим, что вероятность события А изменилась, когда стало известно, что событие B произошло.
Новую вероятность события А, в предположении, что произошло событие B, будем обозначать PB(А).
Таким образом, Р(A)=1/4; PB(А)=1/2
Пусть, например, событие A — появление герба при однократном брссании монеты, а событие B — появление карты бубновой масти при вынимании карты из колоды. Очевидно, что события A и B независимы.
т. е. вероятность совмещения двух независимых событий равна произведению вероятностей этих событий.
События А1, А2, ..., Аn называются независимыми в совокупности, если вероятность наступления каждого из них не меняет своего значения после того, как одно или несколько из остальных событий осуществились.
Дата добавления: 2016-06-22; просмотров: 4064;










