Частотная характеристика сложного двухполюсника.
Входное сопротивление двухполюсника и его входная проводимость есть функции частоты .Зависимости действительной и мнимой частей входного сопротивления или входной проводимости двухполюсника от частоты называют частотными характеристиками двухполюсника.
В том случае ,когда цепь содержит более 2х реактивных элементов ,входное напряжение может совпадать по фазе с входным током на нескольких частотах.
R L2 C1
L1
Это возможно когда два элемента (L1 и C1 ) образуют резонанс токов на частоте ω01= 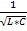 .Сопротивление контура равно ∞ (проводимость равна 0).
.Сопротивление контура равно ∞ (проводимость равна 0).
Второй резонанс на частоте ω02 наступает когда контур L1C1 имеет реактивное сопротивление ёмкостного характера ,которое вместе с L2 образует резонанс напряжений, при котором реактивная составляющая входного сопротивления Х равна 0.
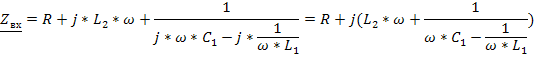
X= 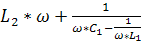
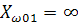
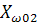 =0=
=0= 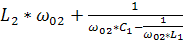 =0
=0
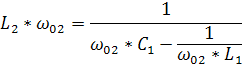
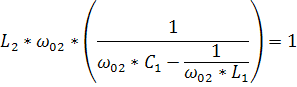
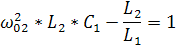
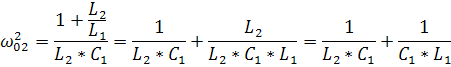
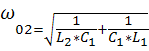
Полное суждения о свойствах такого двухполюсника можно получить если рассматривать его полное сопротивление как функцию частоты .Чаще эту зависимость разбивают на две: активную и реактивную .Для простоты анализа активным сопротивлением часто пренебрегают (R=0).Такой двухполюсник называется реактивным .С частотными характеристиками последовательного и параллельного контуров мы уже познакомились.

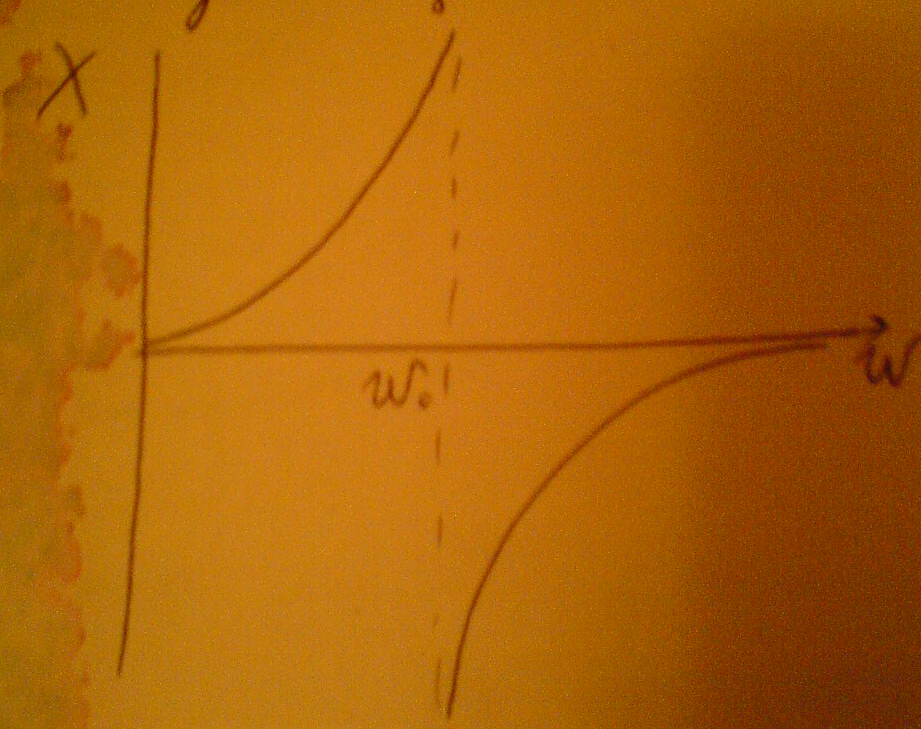
Построим частотную зависимость реактивной составляющей входного сопротивления для нашей схемы. C1
L2
L1
X= 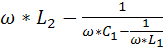
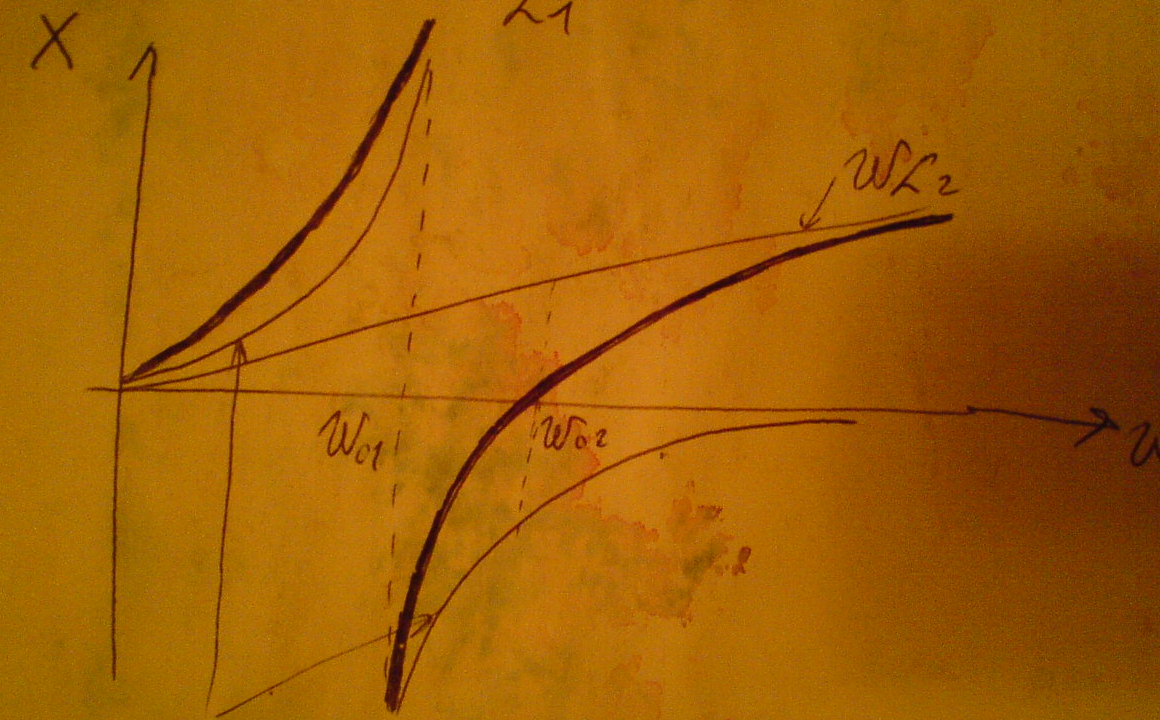
Резонансная частота параллельного участка ω01 (резонанс токов) соответствует полюсу функции ,а резонанс напряжений –соответствует нулю функции. Таким образом мы имеем два резонанса :резонанс токов и резонанс напряжений .Как видно из графика функция Х(ω) всегда возрастает ,т.е 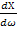 >0 .Из этого следует что не может быть двух подряд резонансов тока или резонанса напряжения ,т.е резонансы чередуются.
>0 .Из этого следует что не может быть двух подряд резонансов тока или резонанса напряжения ,т.е резонансы чередуются.
Для того ,чтобы построить качественно частотную характеристику достаточно определить откуда начинается характеристика при ω=0 ,куда стремится характеристика при ω→ 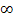 и сколько резонансов она имеет.
и сколько резонансов она имеет.
L1 C1
L2
C2
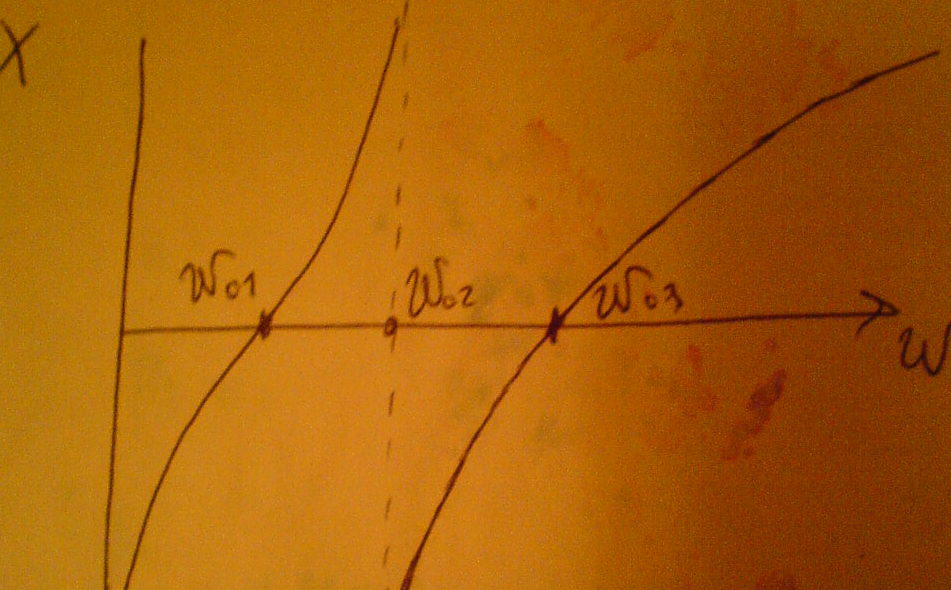
При ω→ 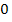 ,Х→-
,Х→- 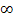
L1 C1
L1
C2
При ω→ 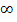 Х→
Х→ 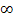
L1 C1
L2
C2
Если постоянный ток не проходит ,то характеристика начинается из - 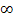 ,в противном случае из 0.Для того чтобы определить число резонансов электрическая схема должна быть сведена к канонической схеме ,т.е параллельно или последовательно включенные однотипные реактивные элементы должны быть заменены одним эквивалентным.
,в противном случае из 0.Для того чтобы определить число резонансов электрическая схема должна быть сведена к канонической схеме ,т.е параллельно или последовательно включенные однотипные реактивные элементы должны быть заменены одним эквивалентным.
C1 C2 → C=C 1 +C2
XL1 X L2 XL= XL1 + X L2
→
Число резонансов в такой схеме на единицу меньше числа реактивных элементов канонической схемы.
Если в схеме есть путь для постоянного тока ,то первым наступит резонанс токов ,если такого пути нет –то первым наступает резонанс напряжений.
Если в схеме есть прямой путь через ёмкость ,то входное сопротивление стремится к 0 при бесконечно большой частоте ,если такого пути нет, то сопротивление стремится к бесконечности.
| <== предыдущая лекция | | | следующая лекция ==> |
| Исследование работы последовательного RLC контура при изменении его параметров и частоты | | | Цепи со взаимной индукцией |
Дата добавления: 2016-05-28; просмотров: 2823;










