Уравнение Эйлера и условия Лежандра для функционалов, зависящих от нескольких функций и от высших производных

Рассмотрим более общий случай, когда функционал зависит от нескольких функций, т. е.

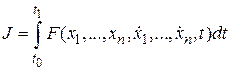(5.3)

и требуется найти функции 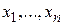, удовлетворяющие граничным условиям

,

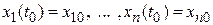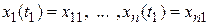
и доставляющие экстремум функционалу.

Варьируя поочередно каждую функцию, входящую в (5.3), при остальных фиксированных, легко получить систему уравнений Эйлера

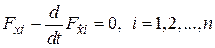(5.4)

где .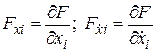

Среди решений системы уравнений (5.4) и отыскиваются функции 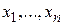, которые удовлетворяют граничным условиям и обеспечивают экстремум функционалу. Постоянные интегрирования 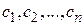определяются по заданным начальным условиям.

Вид экстремума, как и в случае простейшей вариационной задачи с одной функцией, определяется необходимыми условиями Лежандра, которые здесь записываются в виде системы неравенств. Так для достижения функционалом минимума необходимо

.

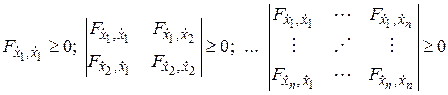В случае минимума знак неравенств меняется на обратный.

Уравнение Эйлера легко обобщается на функционалы, зависящие от высших производных:

.

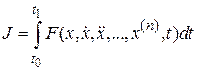Предполагается, что 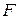– непрерывная функция, дифференцируемая 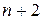раза по всем аргументам, 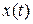– функции, дифференцируемые 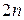раз, а в граничных условиях задаются значения самой функции и ее производных до 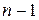включительно.

С помощью тех же рассуждений, что и ранее, условие равенства нулю первой вариации функционала можно связать с уравнением

,

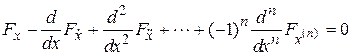известным под названием уравнение Эйлера–Пуассона.