Понятие устойчивости линейной АСР. Необходимое и достаточное условие устойчивости.

На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

В простейшем случае понятие устойчивости системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.

Наблюдения показывают, что некоторые положения равновесия системы устойчивы к небольшим возмущениям, а другие принципиально возможные равновесные положения практически не могут быть реализованы.

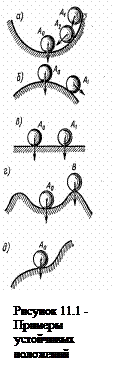
Наглядно устойчивость равновесия представлена на рисунок 11.1, где изображен шар, расположенный в некотором углублении (рисунок 11.1, а), на некоторой выпуклой поверхности (рисунок 11.1, б), на плоскости (рисунок 11.1, в).

Положение равновесия шара характеризуется точкой A₀. В Случае, изображенном на рисунке 11.1, а, при всяком отклонении шара от положения равновесия, например в точку A₁, он будет стремиться снова возвратиться к положению равновесия — в точку A₀ (при отсутствии сил трения) или к некоторой конечной области, окружающей положение равновесия, например в точку A₂ (при наличии сил трения). Такое положение равновесия устойчиво. Случай, изображенный на рисунок 11.1, б, соответствует неустойчивому положению равновесия. Рисунок 11.1, в соответствует безразличному равновесию. На рисунке 11.1, г состояние равновесия устойчиво лишь до тех пор, пока отклонение не вышло за некоторую границу, определяемую, например, точкой В. Выйдя за эту границу, шар уже не вернется в точку A₀, а будет двигаться вправо от точки В либо все время удаляясь, либо до нового состояния равновесия в зависимости от формы поверхности, т. е. в конечном счете в зависимости от уравнений движения шара.

Устойчивость в "малом", в "большом" и в "целом"

Поэтому в общем случае, рассматривая нелинейные системы, вводят понятие устойчивости «в малом», «в большом» «в целом». Система устойчива «в малом», если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Систему называют устойчивой «в большом», когда определены границы области устойчивости, т. е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние, и выяснено, что реальные начальные отклонения принадлежат этой области. В том случае, когда система возвращается в исходное состояние при любых начальных отклонениях, систему называют устойчивой «в целом». Устойчивость «в целом» для определенного класса нелинейностей называют «абсолютной устойчивостью». Так, например, случай, изображенный на рисунке 11.1, а, соответствует устойчивости «в целом», а случай, изображенный на рисунке 11.1, г, может соответствовать либо устойчивости «в большом», либо устойчивости «в малом». Очевидно, что система, устойчивая «в целом», будет устойчива «в большом» и «в малом»; система, устойчивая «в большом», будет устойчива и «в малом».

На рисунке 11.1, д изображено еще одно принципиально возможное для нелинейных систем состояние равновесия, которое называют полуустойчивым.

Для того чтобы дать определение устойчивости равновесия, вводят понятие о невозмущенном состоянии равновесия, соответствующем состоянию покоя в точке A₀ на рисунок 11.1, а, и возмущенном состоянии, соответствующем, например, точке A₁, в которую внешняя сила привела шар и затем прекратила свое действие. Система будет устойчивой, если из возмущенного состояния она перейдет в некоторую заданную область, окружающую невозмущенное состояние равновесия.

В рассмотренном выше примере с шаром вопрос об устойчивости решается довольно просто. Однако следует заметить, что в общем случае далеко не всегда ясно, при каких условиях равновесное положение системы будет устойчивым.

Понятие устойчивости можно распространить и на более общий случай, когда в качестве невозмущенного состояния рассматривают не положение равновесия системы, а ее движение, например движения системы по некоторой наперед заданной траектории.

Допустим, что заданное движение системы при отсутствии возмущений должно определяться некоторым законом изменения независимых координат у₁^*(t), у₂^*(t), ..., y_n^*(t). По аналогии со случаем равновесия положения, заданное движение называют невозмущенным движением.

Внешние возмущения, действующие на систему, вызовут отклонение действительного движения системы от заданного. Действительное движение системы называют возмущенным движением. Пусть действительное движение системы определяется независимыми координатами у₁ (t), у₂ (t), ..., y_n (t). В общем случае y₁(t) ≠ y₁^*(t), y₂(t) ≠ y₂^*(t), … , y_n(t) ≠ y_n^*(t).

Заданное невозмущенное движение будет устойчивым, если после приложения внешних сил (возмущении), которые затем снимают, возмущенное движение по истечении некоторого времени войдет в заданную область | y_i(t) – y_i^*(t )| ≤ ε_i где ε_i = const —заданные величины, i = 1, 2,..., п.

Чтобы проиллюстрировать сказанное, предположим что невозмущенное движение происходит по траектории А, а возмущенное движение происходит по траектории Б (рисунок 11.2, а). Возьмем на этих траекториях две произвольные точки N^А и N^Б, отвечающие одному и тому же моменту времени t.

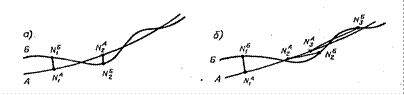
Рисунок 11.2 – Различные виды возмущенного и невозмущенного движения

При устойчивом движении траектория Б должна быть близка к траектории А.

Следует заметить, однако, что близость траекторий А и Б является необходимым условием устойчивости движения, но недостаточным. Действительно, расстояние между точками N^А и N^Б, отвечающими одному и тому же моменту времени, может возрастать не только для расходящихся, но и для близких траекторий (рисунок 11.2, б).

Общая постановка задачи устойчивости по А. М. Ляпунову

Впервые строгое определение устойчивости было дано русским ученым А. М. Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Отсутствие такого определения часто приводило к недоразумениям, так как движение, устойчивое в одном смысле, может оказаться неустойчивым при другом понимании этих слов, и наоборот. Определение устойчивости А. М. Ляпунова оказалось настолько удачным и наилучшим образом удовлетворяющим многим техническим задачам, что оно в настоящее время принято как основное.

Пусть движение системы автоматического управления описывается дифференциальными уравнениями, которые могут быть приведены к виду

dy_i/dt = Y_i(y₁, y₂,…, y_n, t) (11.1)

где y_i - вещественные переменные, характеризующие состояние системы управления (обобщенные координаты); Y_i — известные функции переменных y₁, y₂,…, y_n, и времени t, удовлетворяющие условиям существования и единственности решения.

Исходное состояние системы при t = t₀ однозначно определяется начальными значениями переменных y_i, которые обозначим y₁₀, y₂₀,…, y_n0.

Каждой совокупности начальных значений y₁₀, y₂₀,…, y_n0 соответствует единственное решение (11.1) для всех t > t₀

y_i = y_i(y₁₀, y₂₀,…, y_n0, t) (11.2)

Решение (11.2) описывает какое-либо движение системы, определяемое исходным состоянием.

Некоторое вполне определенное движение системы, подлежащее исследованию на устойчивость, называют невозмущенным движением.

Заметим, что выбор невозмущенного движения является произвольным. Это может быть любое возможное движение системы, как установившееся, так и неустановившееся. Допустим, что в качестве невозмущенного движения выбрано такое, которое описывается заданными функциями времени

y₁ = y₁^*(t),…, y_n = y_n^*(t) (11.3)

Предположим, что функции y_i^* (t) являются частным решением дифференциальных уравнений (1), т. е.

dy_i^* (t)/dt = Y_i(y₁^*, …, y_n^*, t), (11.4)

удовлетворяющим начальным условиям при t = t₀

y₁ = y₁^*(t₀);…; y_n = y_n^*(t₀) (11.5)

В частном случае, когда параметры системы не изменяются со временем и функции Y_i не зависят явно от t, движения (11.3) являются установившимися. Им отвечают решения

y_i^* = const, (11.6)

служащие корнями уравнений

Y_i (y₁, y₂,…, y_n) = 0 (11.7)

Изменим условия (11.5), дав начальным значениям переменных y₁, y₂,…, y_n небольшие по модулю приращения ε₁, ε₂,…, ε_n т. е. пусть при t = t₀

y₁ = y₁^*(t₀) + ε₁; y₂ = y₂^*(t₀) + ε₂;…; y_n = y_n^*(t₀) + ε_n (11.8)

Движение системы, отвечающее измененным начальным условиям (11.8), называют возмущенным движением. Другими словами, возмущенным движением системы называют всякое иное движение системы, отличное от невозмущенного. Введем новые переменные

x_i(t) = y_i(t) – y_i^*(t), (11.9)

равные разности переменных y_i в возмущенном и невозмущенном движении. Переменные x_i называют отклонениями или вариациями величин y_i. Если все отклонения равны нулю

x₁ = 0; x₂ = 0;…; x_n = 0 (11.10)

то возмущенное движение y_i(t) будет совпадать с невозмущенным движением y_i^*(t), т. е. невозмущенному движению отвечают нулевые значения переменных x_i.

Пусть при t = t₀ переменные x_i принимают какие-либо начальные значения x_i0 , из которых по крайней мере одно не равно нулю:

x_i = х_i0 = ε_i (11.11)

Начальные значения отклонений (11.11) называют возмущениями.

А. М. Ляпуновым было дано следующее определение устойчивости: невозмущенное движение называют устойчивым по отношению к переменным х_i если при всяком произвольно заданном положительном числе ε, как бы мало оно ни было, можно выбрать другое такое положительное число δ(ε), что при всяких возмущениях x_i0, удовлетворяющих условию

∑x_i0² ≤ δ, (11.12)

и при любом t ≥ t₀ будет выполняться неравенство

∑x_i²(t) < ε, (11.13)

в противном случае движение неустойчиво.

Определению устойчивости А. М. Ляпунова можно дать следующую геометрическую интерпретацию. Совокупность отклонений x₁, x₂,…, x_n в n-мерном пространстве, переменных x₁, x₂,…, x_n определяет точку M (ее называют изображающей точкой). В возмущенном движении при изменении величин x₁, x₂,…, x_n изображающая точка будет описывать некоторую траекторию. Невозмущенному движению x_i = 0 отвечает неподвижная точка — начало координат.

Рассматривая, например, случай, когда i= 3, построим в трехмерном пространстве координат x_i две сферы: сферу ε = ∑ x_i² с радиусом 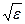и сферу δ = ∑ x_i0² с радиусом 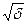. Выберем радиус сферы ε произвольно малым. Если невозмущенное движение устойчиво, то для этой сферы должна найтись другая сфера δ, обладающая следующим свойством; изображающая точка М, начав свое движение из любой точки М₀, лежащей внутри или на поверхности сферы δ, при своем дальнейшем движении остается всегда внутри сферы ε, никогда не достигая ее поверхности (рисунок 11.3).

Если же невозмущенное движение неустойчиво, то траектория изображающей точки М с течением времени пересечет сферу ε изнутри наружу (или попадет на ее поверхность) при сколь угодно близком положении точки М₀ к началу координат.

Заметим, что при i > 3 надо рассматривать движение изображающей точки в многомерном пространстве относительно гиперповерхностей (гиперсфер) и рассмотрение теряет наглядность.

Практически устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения. Если невозмущенное движение неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.

Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, т. е.

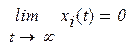
то невозмущенное движение называют асимптотически устойчивым.

При асимптотической устойчивости изображающая точка течением времени должна неограниченно стремиться к началу координат, не выходя из сферы ε.

Отметим некоторые особенности определения устойчивости по А. М. Ляпунову. Во-первых, предполагают, что возмущения налагаются только на начальные условия, иначе говоря, возмущенное движение происходит при

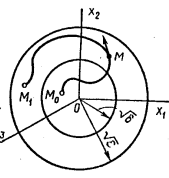
Рисунок 11.3 – Устойчивость по Ляпунову

тех же силах (источниках энергии), что и невозмущенное движение, Во-вторых, устойчивость рассматривают на бесконечно большом промежутке времени. В-третьих, возмущения предполагаются малыми. Несмотря на эти ограничения, определение А. М. Ляпунова устойчивости движения является эффективным и плодотворным в приложениях.

Когда известно общее решение дифференциальных уравнений движения (11.1) можно непосредственно определить значения переменных y_i(t) в возмущенном движении, составить вариации x_i(t) = y_i(t) – y_i^*(t) и, исследуя их, решить вопрос об устойчивости невозмущенного движения у_i^*(t). Однако, как правило, исследование устойчивости движения производят не путем анализа общего решения, а методами, основанными на качественном анализе дифференциальных уравнений возмущенного движения, которым удовлетворяют отклонения (вариации) x_i.

Чтобы вывести уравнения возмущенного движения, найдем из (11.9) переменные y_i(t) = y_i^*(t) + x_i(t) и подставим эти значения y_i(t) в дифференциальные уравнения движения (11.1). Тогда

dy_i^*(t)/dt + dx_i(t)/dt = Y_i(y₁^*+ x₁, y₂^*+ x₂,…, y_n^*+ x_n, t) (11.15)

Если правые части уравнений (11.15) допускают разложение в степенные ряды Тейлора, то после этого разложения по степеням х, получим

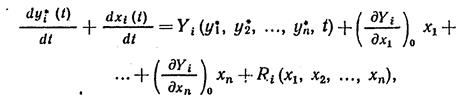(11.16)

где R_i(x₁, x₂,…, x_n ) — совокупность членов, зависящих от отклонений x_i в степени выше первой. Учитывая (11.4), будем иметь

dx_i(t)/dt = a_i1x₁ + a_i2x₂ +...+a_inx_n + R_i (x₁, x₂,…,x_n). (11.17)

В уравнениях (11.17) коэффициенты

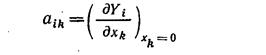
в общем случае являются функциями времени t; в частности, они могут быть постоянными. В дальнейшем, если не будет оговорено особо, будем считать коэффициенты a_ik постоянными. Уравнения (11.17) называют дифференциальными уравнениями возмущенного движения.

Если отклонения x_i достаточно малы, то, пренебрегая R_i (x₁, x₂,…,x_n), получим линеаризованные уравнения

ax_i /dt =a_i1x₁ + a_i2x₂ + …a_inx_n, , i = 1, 2, ..., п, (11.19)

называемые уравнениями первого приближения.

Необходимое и достаточное условия устойчивости АСР

Во многих случаях устойчивость движения исследуют по уравнениям первого приближения. Это объясняется не только простотой этого метода, но также и тем, что знания процессов, происходящих в реальных системах, позволяют надежно определять только первые линейные члены. Однако на основании уравнений первого приближения можно дать иногда неверное заключение об устойчивости движения. Поэтому, естественно, возникает вопрос об определении условий, при выполнении которых по уравнениям первого приближения можно дать правильные ответы об устойчивости движения. Эту исключительно важную и принципиальную для теории автоматического управления задачу впервые поставил и решил А. М. Ляпунов.

Системе уравнений (11.19) соответствует характеристическое уравнение, которое можно записать следующим образом:

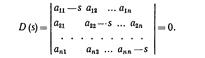(11.20)

Из (11.20) можно найти его корни s_i, где i =1, 2,..., п, которые в общем случае имеют вид s_i = α_i ± jω_i где α_i и ω_i — вещественные и мнимые части корней соответственно.

Для исследования устойчивости систем по их линеаризованным уравнениям принципиально важны следующие теоремы А. М. Ляпунова, которые приведем без доказательства.

Теорема 1. Если вещественные части всех корней s_i характеристического уравнения (11.20) первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.

Теорема 2. Если среди корней s_i характеристического уравнения (11.20) первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.

Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют критическим. Как показал Ляпунов, в критическом случае устойчивость (неустойчивость) невозмущенного движения не может быть оценена по уравнениям первого приближения, так как она зависит от вида нелинейной функции R_i (x₁, x₂,…,x_n) и поэтому в этом случае требуется рассмотрение дифференциальных уравнений возмущенного движения (11.17) в их исходном виде.

Теоремы Ляпунова имеют весьма важное значение, так как они позволяют судить об устойчивости нелинейных систем по их линеаризованным уравнениям (уравнениям первого приближения)