Изменение вектора правых частей ограничения.

Во многих случаях ограничения трактуются как условия ограниченности ресурсов. В таком случае, правая часть ограничений является верхней границей количества доступных ресурсов.

Допустим, что есть ограничение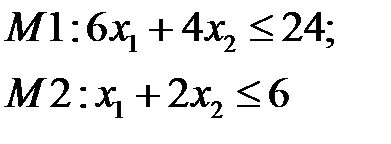

Графическое представление решения задачи приведено на рис.

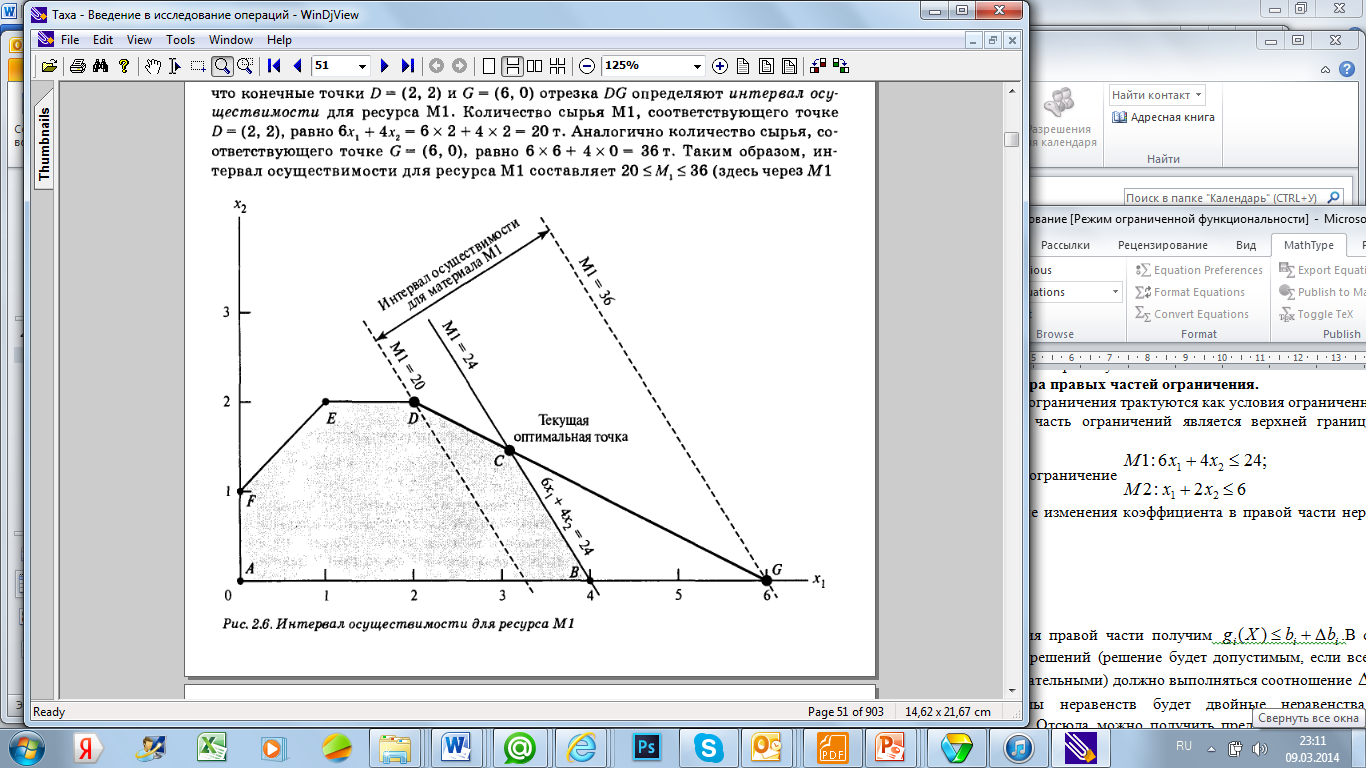
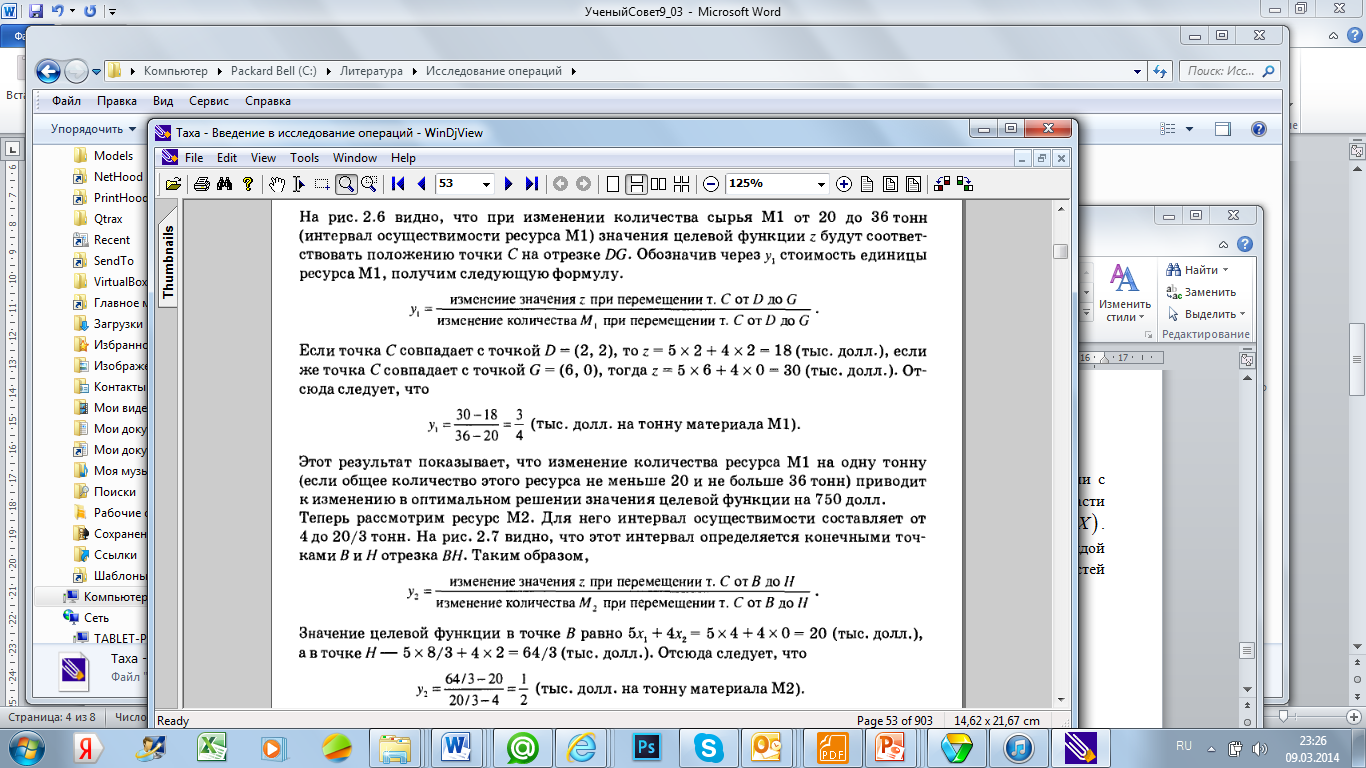
При изменении уровня доступности первого вида ресурсов точка С оптимального решения плавно «плывет» по линии DG. Любое значительное увеличение данного ресурса выводит точку С из этой прямой. Таким образом, изменяется решение.

Поэтому можно указать конечные точки D(2,2), G(6,0). Значение ресурса для первой из этих двух точек равно 20. Для второй – равно 36. Таким образом, интервал осуществимости для ресурса М1 .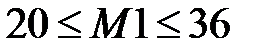

Если мы обозначим 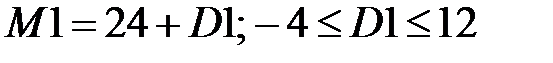. Это означает, что ресурс может быть уменьшен на 4 или увеличен на 12. В том случае можно гарантировать, что решение будет находиться в точке пересечения ограничений ресурсов М1 и М2.

Аналогичную ситуацию можно представить и для второго ограничения.

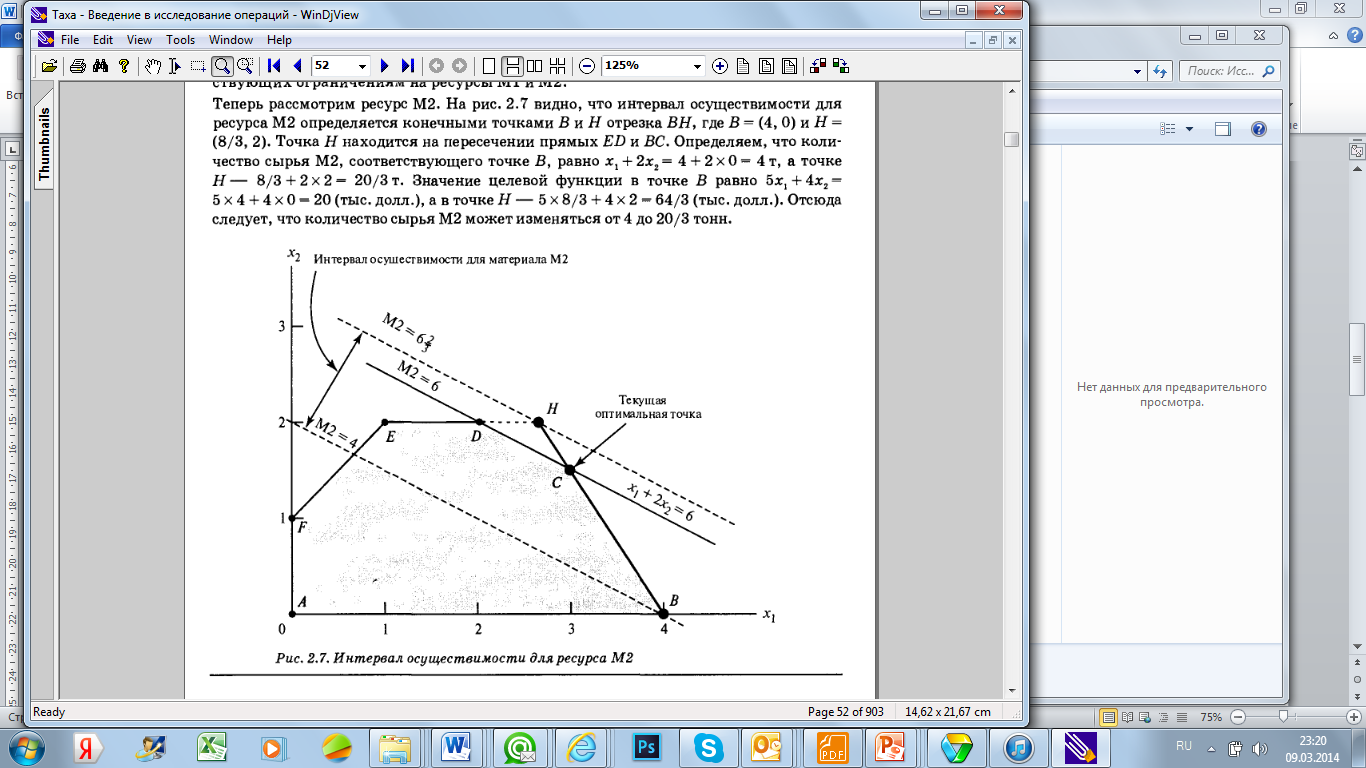
Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн.

Рассмотрим влияние изменения коэффициента в правой части неравенств. Пусть неравенство имеет вид

.

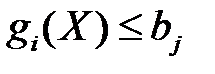С учетом изменения правой части получим 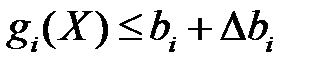.В соответствии с признаком допустимости решений (решение будет допустимым, если все правые части неравенств будут неотрицательными) должно выполняться соотношение 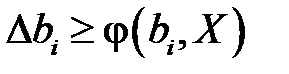. Решением такой системы неравенств будет двойные неравенства для каждой 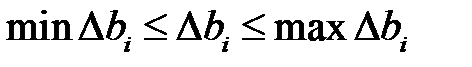. Отсюда можно получить пределы изменения правых частей каждого ограничения, чтобы оптимальный план не изменился

.

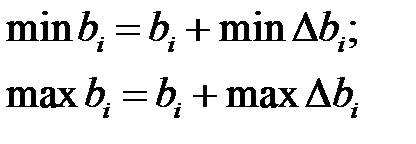Определим стоимость ресурсов. Обозначим стоимость ресурсов

Стоимость ресурса будет решением двойственной задачи линейного программирования.

2 Изменение коэффициентов целевой функции. Необходимо найти решение серии задач линейного программирования,

Для приведения данной задачи к стандартной форме введем дополнительные переменные

В результате оптимизации получим симплекс таблицу. Пусть в ней каждый коэффициент в целевой функции при базисных переменных имеет вид 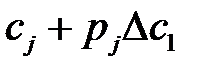. Так как каждый коэффициент должен быть неотрицательным, поэтому получаем систему неравенств вида 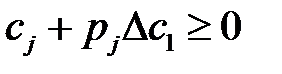. Решив эту систему, можно определить двойное неравенство, ограничивающее сверху и снизу диапазон 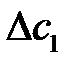. Данное неравенство определяет пределы изменения коэффициента целевой функции, при которых сохраняется структура оптимального плана.

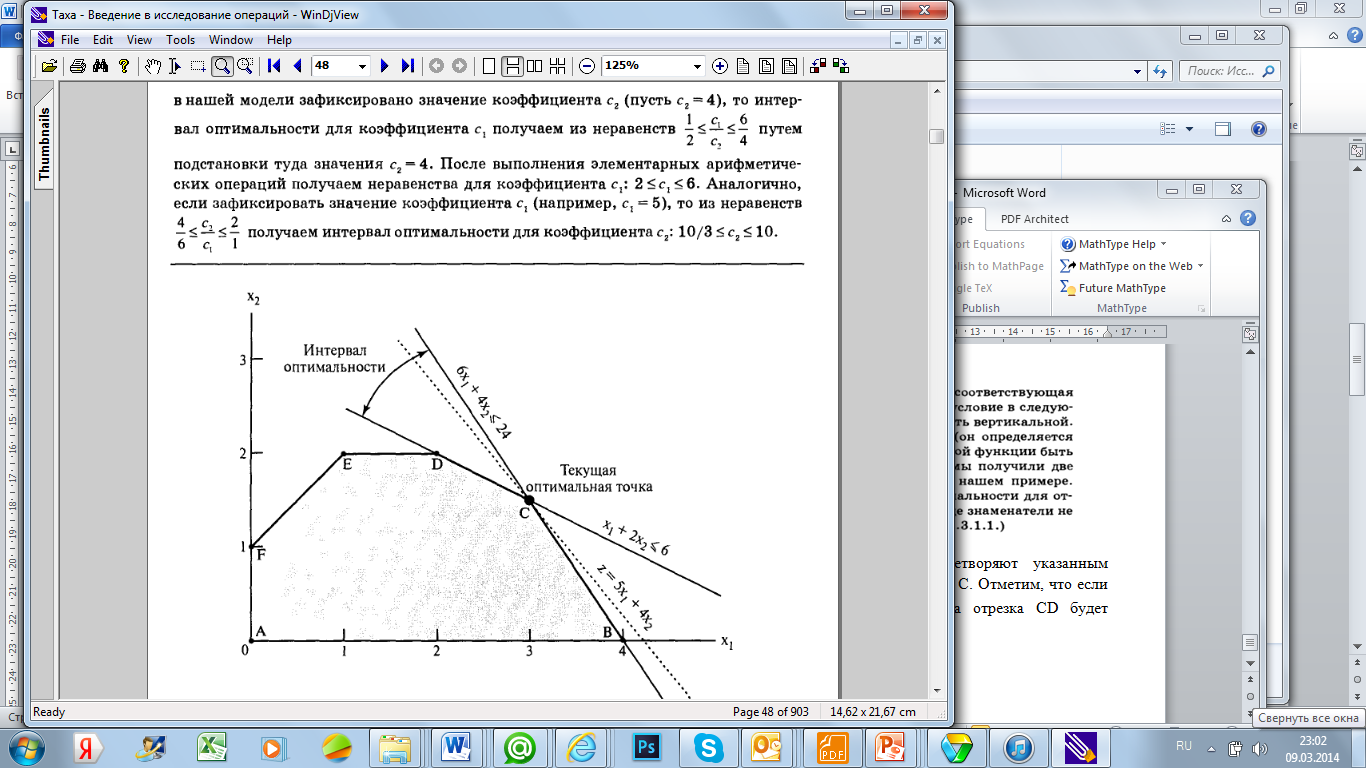
Рассмотрим графическое решение проблемы чувствительности. Пусть целевая функция имеет вид: 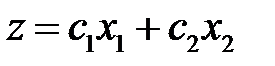. Изменение коэффициентов в целевой функции приводит к изменению угла наклона, что может привести к изменению решения: оно будет достигаться в другой угловой точке. Вместе с тем, очевидно, сохраняется некоторое соотношение коэффициентов, при которых текущее оптимальное решение сохраняется.

Решим задачу в Excel.

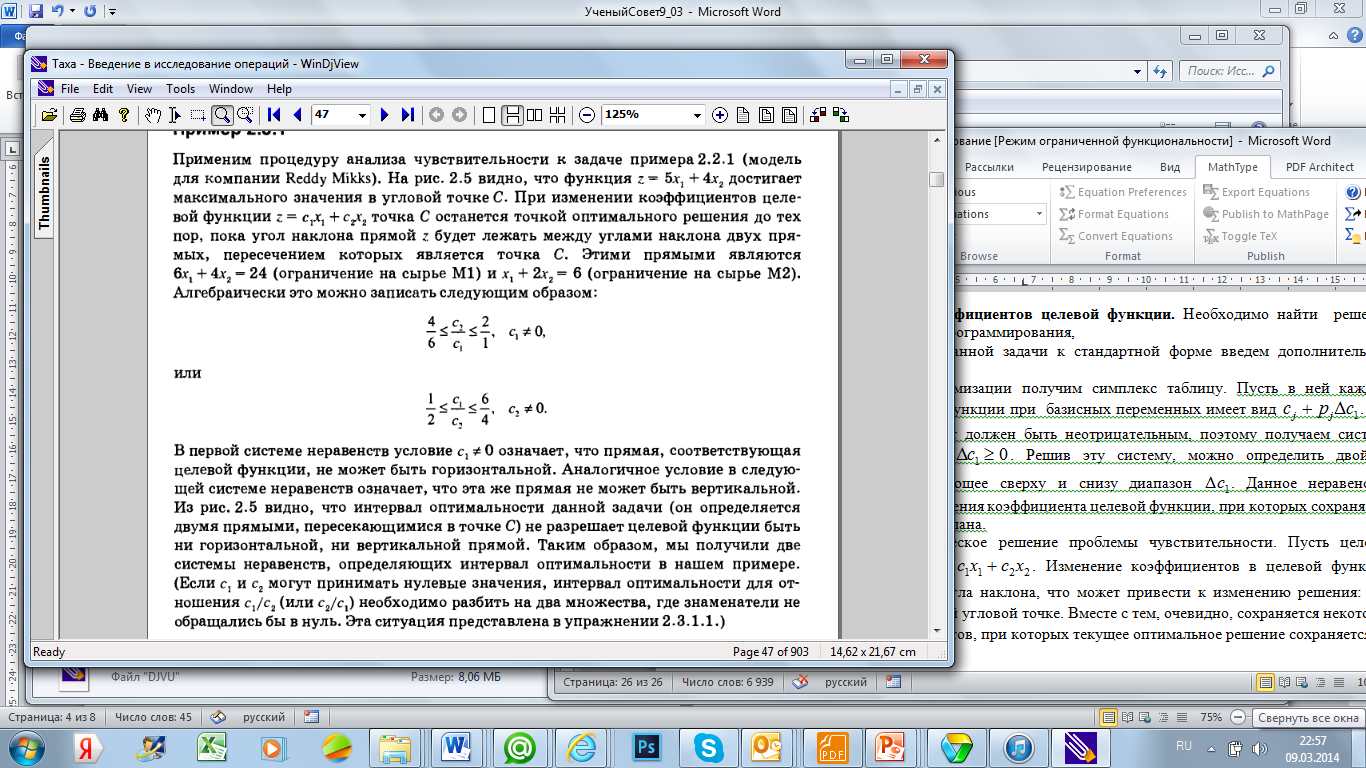
Итак, если коэффициенты в целевой функции удовлетворяют указанным ограничениям, то оптимальное решение будет находиться в точке С. Отметим, что если 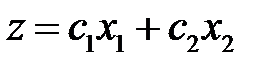совпадет с прямой 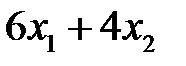, то любая точка отрезка CD будет оптимальным решением.

Приведенные выше неравенства могут быть использованы при определении интервала оптимальности для какого –либо коэффициента в целевой функции, если другой коэффициент известен и остается неизменным. Например. Если в нашем случае зафиксировано значение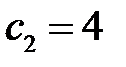

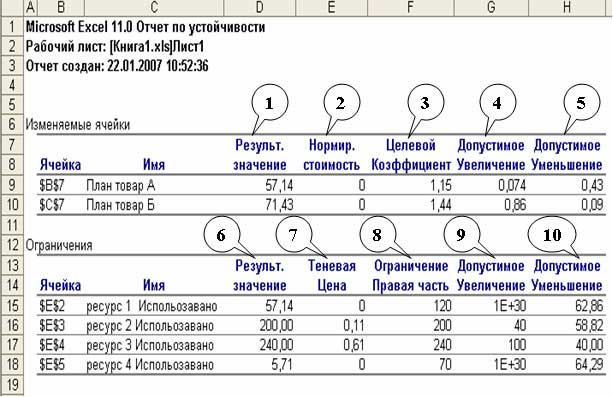
Отчет по устойчивости (более точным за содержанием был бы перевод с оригинала sensitivity - чувствительность) есть наиболее интересным и полезным – он определяет чувствительность структуры полученного плану до изменений начальных данных и, согласно, дальнейшие действия менеджера с целью улучшения результатов. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа.

1 – оптимальный план задачи. В нашем случае, чтобы получить максимальную выручку в размере 168,37 д. ед., нужно производить 57,14 единиц товара А и 71,43 единиц товара Б;

2 – нормированная стоимость касается неизвестных плана. Это неудачный перевод с оригинала reduced cost, которую можно было перевести, как «цена, которая уменьшает (целевую функцию)». Этот показатель, как изменится оптимальное значение ЦФ при выпуске продукции, которой нету в оптимальном плане. Например, если нормированная стоимость товара А была бы -3 (хотя в нашем случае это 0), то принудительный выпуск 2 единиц товара А, которых нету в оптимальном плане привел к уменьшению Дохода на 2•3=6 и составлял бы 168,57-6= 162, 57 д. ед.

3 – коэффициенты ЦФ;

4, 5 – границы изменений значений коэффициентов ЦФ при условии, что количество оптимальной продукции (план) не изменится. Например, если целевой коэффициент товара А (КА) равен 1,15 (цена за 1 единицу товара), то изменяя его в рамках 1,15-0,43< КА<1,15+0,074 > 0,72< КА<1,224 план не изменится, но значения дохода может уменьшится или увеличится. Это можно проверить, если запустить программу «Поиск решений», после внесений в таблицу изменений данного коэффициента.

6 – количество использованных ресурсов;

7 – теневая цена (в нелинейной модели это множитель Лагранжа) касается ограничений, то есть, определенное значение указывает на «ценность» ограниченного ресурса в сравнении с другими ресурсами. Этот показатель указывает, как изменится оптимальное значение ЦФ (Доход) при изменении запасов ресурсов на 1 единицу. Например, если увеличить запас ресурса 3 на 10 единиц, то доход увеличится на 10•0,61=6,1 и будет составлять 168,57+6,1=174,67 д. ед.

8 – запасы ресурсов;

9, 10 – задают диапазон для 8, в котором действует теневая цена 7 (аналогично 4, 5). Например, диапазон ресурса 3: 200<ресурс 3<340. Если ресурс 3 увеличить на 10 единиц, то доход увеличится на 6,1 и будет составлять 174,67. Если этот ресурс увеличить на 110 единиц, то про доход ничего сказать нельзя, поскольку мы вышли за указанные пределы.

Вывод:для конечного результата оптимизации нужен только отчет по устойчивости плана, поскольку там содержится наиболее существенная информация.

ОТЧЕТ по пределам состоит из Двух частей, что касаются значений ЦФ (Целевое) и плана (Изменяемое).

1 - значение ЦФ (Доход);

2 - оптимальный план задачи;

3 - наименьшее значения, которое может принять неизвестное (в нашем случае количество товара А и Б имеет Нижний предел 0, поскольку мы в Параметрах Поиска решений отметили Неотрицательные значения);

4 - это значение, которое будет в целевой ячейке (Доход), если неизвестное будит равно Нижнему пределу;

5 - это наибольшее значение, которое может содержать неизвестные , чтобы получить максимальную ЦФ;

6 - это значение, которое будет в целевой ячейке (Доход), если неизвестные будут равны Верхнему пределу. Вывод: как видим, отчет по пределам содержит результаты, которые мы уже имеем в таблице, потому его можно в дальнейшем не выводить.

Отчет по результатам содержит информацию о трех компонентах задачи оптимизации: целевой функции (Целевая ячейка), плана (Изменяемые ячейки), и ограничений (Ограничения).

1 – начальное значение целевой функции при начальном опорном плане (3);

2 – максимальное или минимальное значение (в зависимости от задачи) целевой функции. В нашем случае - 168,57 д. ед.;

3 – начальный опорный план;

4 – оптимальный план задачи. В нашем случае, чтобы получить максимальную выручку в размере 168,37 д. ед., нужно производить 57,14 единиц товара А и 71,43 единиц товара Б (понятно, что товар должен быть в целых единицах, но если бы мы задали такой параметр, то не получили отчеты, которые нужны для анализа и улучшение полученных результатов);

5 – показывает количество использованных ресурсов на производство при оптимальном плане;

6 – формулы ограничений;

7 – показывает влияние ограничений на конечный результат. Если статус «связанное», тогда данное ограничение влияет на полученный план, если «не связан» - значит не влияет. В нашем случае ресурс 1 и 4 имеют статус «не связан» - это значит, что эти ресурсы не ограничивают возможности в производстве, что не скажешь про ресурс 2 и 3, которые использованы полностью;

8 – разница между имеющемся в наличие количеством ресурсов и использованных при полученном плане.

Вывод: большинство данных отчета занесены в таблицу, другие – просто не нужны для анализа. Значит этот вид отчета можно не выводить!