ПОНЯТИЕ ДВОЙСТВЕННОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Симплекс-метод является универсальным. С его помощью может быть решена любая задача линейного программирования. Однако в силу своей универсальности, он не свободен от некоторых недостатков. В ряде случаев для решения задач линейного программирования более подходящими оказываются так называемый двойственный метод. Этот метод базируется на теории двойственности, одной из важнейших составных частей общей теории линейного программирования.
Теория двойственности используется для разработки методов решения многих практически важных классов линейных оптимизационных задач: задач транспортного типа, линейных целочисленных задач и т.д. Рассмотрим основные положения этой теории.
Каждой задаче линейного программирования соответствует другая задача, в определенном смысле ей противоположная. Если первая задача называется прямой, то противоположная - двойственной. Так как двойственная по отношению к двойственной задаче - это исходная прямая задача, то неважно, какую из задач назвать прямой, а какую двойственной. Поэтому прямую и двойственную задачи называют задачами двойственной пары.
Двойственная задача формулируется непосредственно из прямой с помощью определенных правил. Поскольку прямые задачи могут иметь ограничения в виде неравенств типа  , типа
, типа  или в виде равенств, то и правила получения двойственных задач для них оказываются различными.
или в виде равенств, то и правила получения двойственных задач для них оказываются различными.
Выделяют симметричные, несимметричные и смешанные двойственные задачи. В симметричных задачах ограничения прямой задачи имеют вид 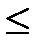 . В ограничениях несимметричной задачи в ограничениях прямой задачи используются знаки равенства. В смешанных задачах используются оба вида отношений «меньше или равно» и «Равно». В несимметричных и смешанных задачах на вновь вводимые переменные не накладывается требование их неотрицательности.
. В ограничениях несимметричной задачи в ограничениях прямой задачи используются знаки равенства. В смешанных задачах используются оба вида отношений «меньше или равно» и «Равно». В несимметричных и смешанных задачах на вновь вводимые переменные не накладывается требование их неотрицательности.
Вычисления, основанные на соотношениях двойственности, начинаются с приведения прямой и двойственной задачи к стандартной форме. Поэтому можно ограничиться формулировкой правил образования задачи двойственной по отношению к стандартной задаче линейного программирования. Правила получения двойственной задачи для других видов задачи ЛП могут быть получены из данных правил.
Запишем задачу ЛП в стандартной форме:
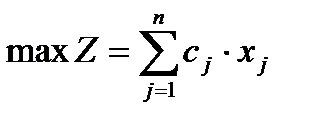 ,
,
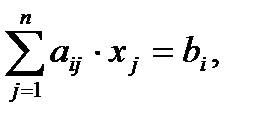
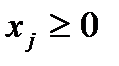 ,
,
i=1,..,m; j=1,..,n.
Назовем эту задачу прямой. Тогда двойственной по отношению к ней будет задача:
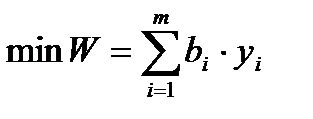 ,
,
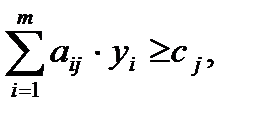
i=1,..,m; j=1,..,n.
Проанализировав задачи, можно сделать следующие выводы:
1. Каждому ограничению прямой задачи соответствует переменная двойственной задачи.
2. Каждой переменной прямой задачи соответствует ограничение двойственной задачи.
3. Коэффициенты при какой-либо переменной в ограничениях прямой задачи становятся коэффициентами ограничения двойственной задачи, соответствующей этой переменной, а правая часть формируемого ограничения равна коэффициенту при этой переменной в выражении целевой функции.
4. Вид экстремума двойственной задачи противоположен виду экстремума прямой задачи;
5. Векторы В и С в прямой и двойственной задачах меняются местами;
6. Матрица A двойственной задачи получается путем транспонирования матрицы А прямой задачи;
7. Все ограничения двойственной задачи имеют вид  для задачи максимизации и вид
для задачи максимизации и вид  для задачи минимизации линейной формы.
для задачи минимизации линейной формы.
Для случая симметричной двойственной задачи:
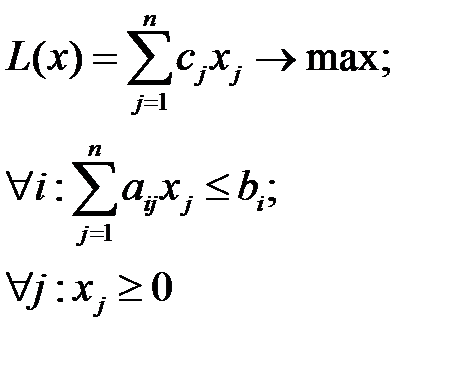
Двойственная задача имеет вид:
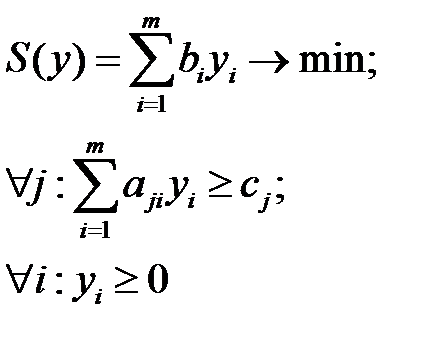
Для случая несимметричной задачи:
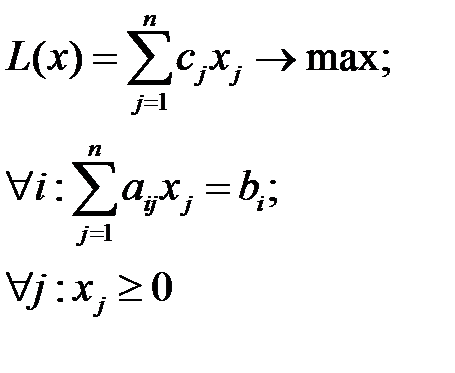
Двойственная задача имеет вид:

Смешанные задачи содержат ограничения в виде равенств и неравенств. При составлении двойственной задачи необходимо использовать правила перехода для симметричной и несимметричной задач.
Приведенные ниже примеры служат иллюстрацией правил получения двойственных задач.
Пример Дана задача линейного программирования (слева от каждого ограничения стоит ассоциированная с ним двойственная переменная). Данная задача относится к несимметричной.
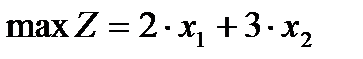
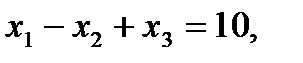
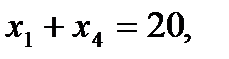
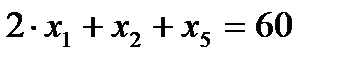 ,
,
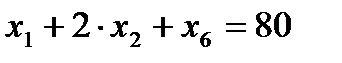
 .
.
Сформулируем для этой задачи двойственную задачу. Целевая функция двойственной задачи представляет собой линейную форму, полученную как произведение вектора b=(10,20,60,80) на вектор переменных двойственной задачи Y =( 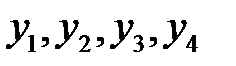 ). Кроме того, поскольку в прямой задаче целевая функция максимизируется, в двойственной она минимизируется. С учетом сделанных замечаний получим,
). Кроме того, поскольку в прямой задаче целевая функция максимизируется, в двойственной она минимизируется. С учетом сделанных замечаний получим,
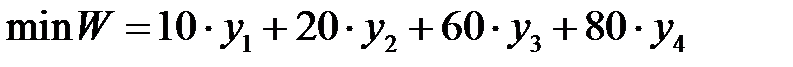 ,
,
Левая часть первого ограничения двойственной задачи представляет собой произведение вектора системы ограничений прямой задачи, ассоциированного с переменной 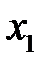 , на вектор переменных двойственной задачи. Правая часть этого ограничения равна коэффициенту при переменной
, на вектор переменных двойственной задачи. Правая часть этого ограничения равна коэффициенту при переменной 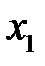 , в целевой функции прямой задачи.
, в целевой функции прямой задачи.
А поскольку к тому же, прямая задача является задачей поиска максимума, то первое ограничение имеет вид:
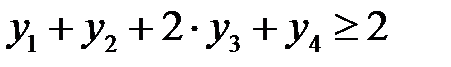
Рассуждая аналогично, получим второе ограничение двойственной задачи: 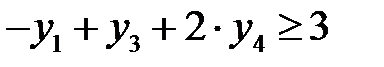 . Отсутствие переменной
. Отсутствие переменной 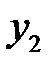 в этом ограничении связано с тем обстоятельством, что во втором ограничении прямой задачи нет переменной
в этом ограничении связано с тем обстоятельством, что во втором ограничении прямой задачи нет переменной 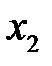 .
.
Переменная  , ассоциированная с третьей переменной двойственной задачи, встречается только в первом ограничении прямой задачи. По этой причине для третьего ограничения получим
, ассоциированная с третьей переменной двойственной задачи, встречается только в первом ограничении прямой задачи. По этой причине для третьего ограничения получим 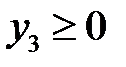 . Рассуждая по аналогии, получим четвертое, пятое и шестое ограничения:
. Рассуждая по аналогии, получим четвертое, пятое и шестое ограничения: 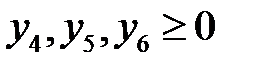 .
.
Таким образом, не смотря на то, что на переменные двойственной задачи условие не отрицательности специально не накладывалось, тем не менее, для всех их оно оказалось выполненным.
Пример Дана задача линейного программирования в нестандартной форме
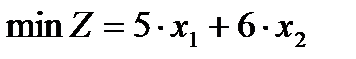 ,
,
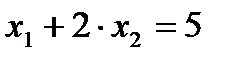 ,
,
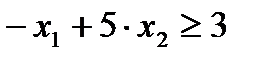 ,
,
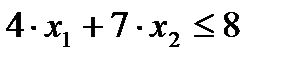 ,
,
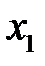 не ограничена в знаке,
не ограничена в знаке,  .
.
Запишем эту задачу в стандартной форме. Для этого сделаем замену переменных 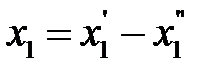 , введем во второе ограничение избыточную переменную
, введем во второе ограничение избыточную переменную 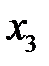 , а в третье - добавочную переменную
, а в третье - добавочную переменную 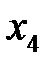 . Получим
. Получим
 ,
,
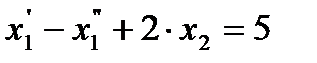 ,
,
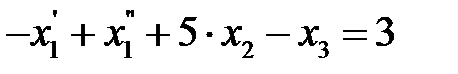 ,
,
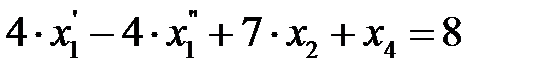 ,
,
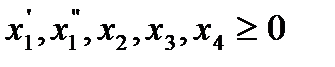 .
.
Сформулируем двойственную задачу. Поскольку в прямой задаче целевая функция минимизируется, целевая функция двойственной задачи имеет вид 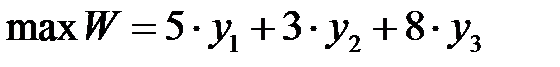 .
.
По этой же причине первое, второе и третье ограничения двойственной задачи, ассоциированные соответственно с переменными  записываются следующим образом:
записываются следующим образом:
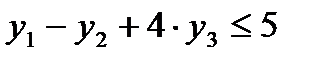 ,
,
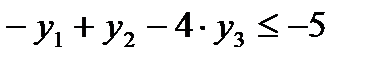 ,
,
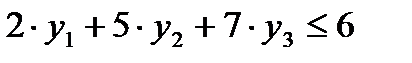 .
.
Поскольку переменная 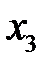 встречается только во втором, а переменная
встречается только во втором, а переменная 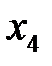 - только в третьем уравнении прямой задачи, ассоциированные с ними ограничения двойственной задачи имеют вид:
- только в третьем уравнении прямой задачи, ассоциированные с ними ограничения двойственной задачи имеют вид:
 .
.
Таким образом, из трех переменных двойственной задачи одна - 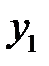 оказалась неограниченной в знаке.
оказалась неограниченной в знаке.
С помощью теорем двойственности, зная решение одной из задач можно найти оптимальное решение другой не решая ее.
Рассмотрим смешанную задачу.
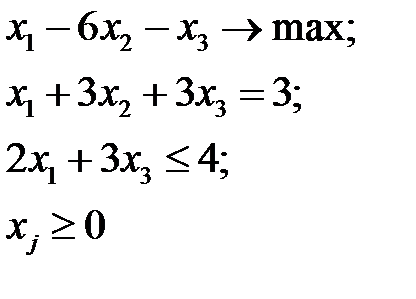
Двойственная для нее задача будет иметь вид:
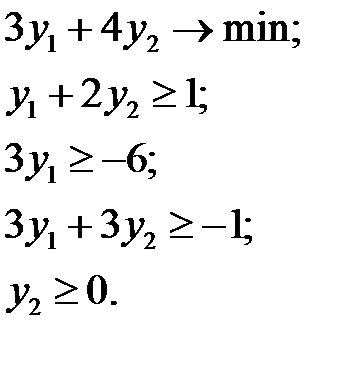
Если использовать каноническую форму задачи линейного программирования, то имеем дело с несимметричной задачей линейного программирования.
Пример

Каноническая форма задачи имеет вид:
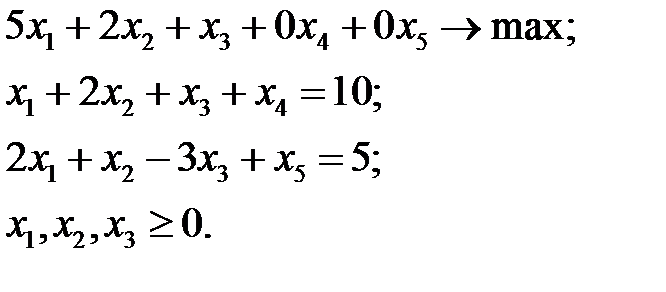
Двойственная задача будет иметь вид:
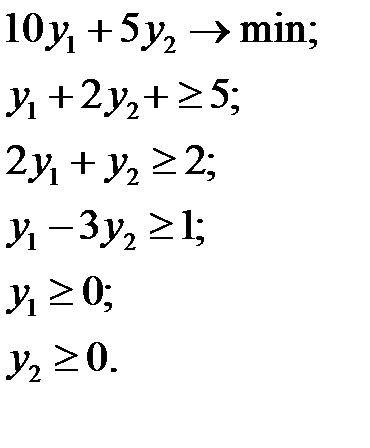
Теорема 1. Для любой пары допустимых решений прямой и двойственной задач значение целевой функции в задаче максимизации не превосходит значения целевой функции в задаче минимизации.
Практическая ценность этой теоремы заключается в следующем. На практике иногда лучше получить решение, близкое к оптимуму, но за малое время, чем оптимальное - но за время, существенно большее. В этом случае последнее неравенство может служить оценкой близости решения, полученного на очередной итерации, к оптимуму.
Теорема 2. Если одна из двойственных задач имеет оптимальное решение, то другая тоже имеет оптимальное решение, причем значения целевых функций для обеих решений совпадают. Если одна из двойственных задач имеет неограниченную целевую функцию, то другая неразрешима, т.е не имеет допустимых решений.
Теорема. Для оптимальности допустимых решений необходимо и достаточно, чтобы они удовлетворяли системе уравнений
 .
.
Данная теорема означает, что одна из переменных какой-либо из задач строго больше нуля, то соответствующее ей ограничение в другой двойственной задаче выполняется как строгое равенство, и, наоборот, если при оптимальном решении какое-либо ограничение выполняется как строгое неравенство, то соответствующая ему переменная в оптимальном решении равна нулю.
Пример Решим симметричную задачу. Пусть исходная задача имеет вид
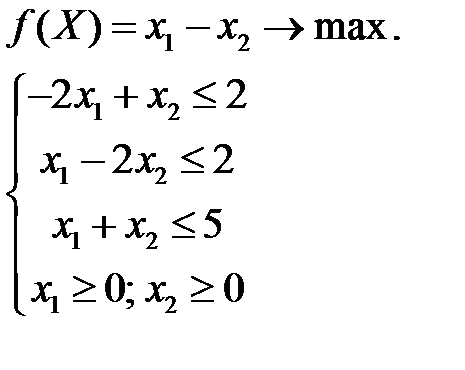
Решив задачу графическим методом, получим 
Составим для нее двойственную задачу
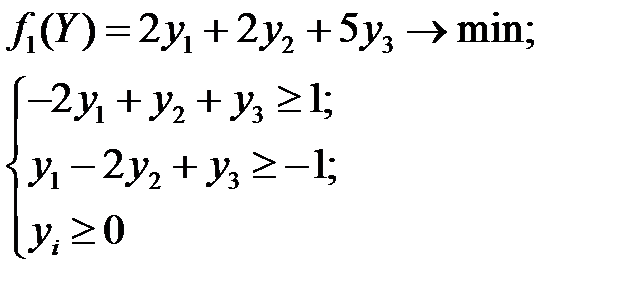
Так целевые функции в точке оптимума равны, то 
Так как переменные 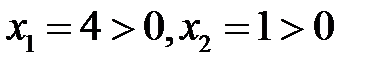 , то соответствующие им ограничения в двойственной задаче содержат знак равенства. Данные ограничения имеют вид
, то соответствующие им ограничения в двойственной задаче содержат знак равенства. Данные ограничения имеют вид
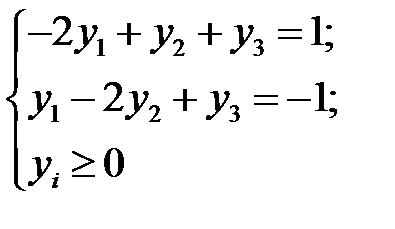
Подставим в ограничения значения 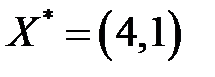 . Получим
. Получим
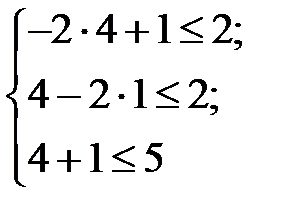 .
.
В данной системе только первое неравенство является строгим. Следовательно, 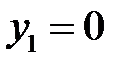 . Другие значения переменных найдем из системы уравнений
. Другие значения переменных найдем из системы уравнений
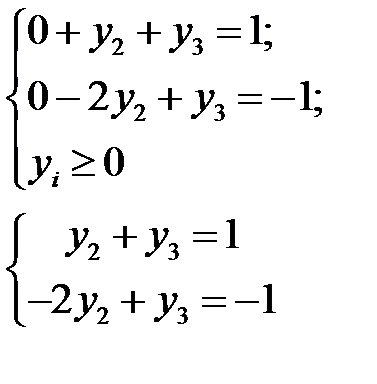 .
.
В результате решения данной системы линейных алгебраических уравнений, получим 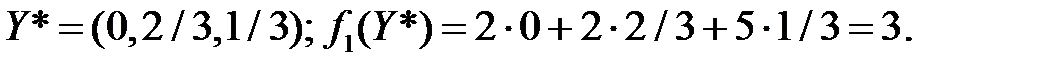
Решим ту же задачу, однако считая, что известно решение 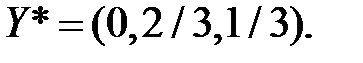
Так как вторая и третья переменные строго больше нуля, то соответствующее им ограничение выполняется как строгое равенство.
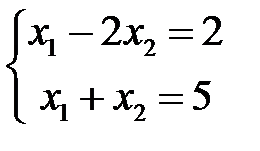 .
.
Решая данную систему уравнений, получим 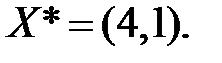
Если исходная задача решена симплексным методом и в итоговой целевой функции получены коэффициенты  - матрица – строка коэффициентов, то решение двойственной задачи может быть найдено по формуле
- матрица – строка коэффициентов, то решение двойственной задачи может быть найдено по формуле 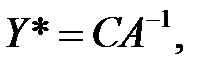 где
где 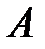 -матрица коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи.
-матрица коэффициентов при базисных переменных целевой функции в оптимальном решении исходной задачи.
Рассмотрим экономическую интерпретацию двойственной задачи.
Теорема. Значения переменных 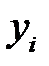 в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов ограничений исходной задачи на оптимальное значение ее целевой функции. Так как
в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов ограничений исходной задачи на оптимальное значение ее целевой функции. Так как
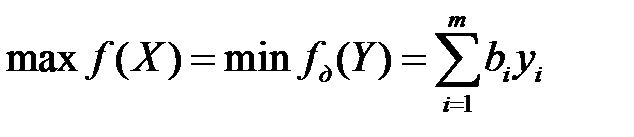
То двойственные переменные показывают, как изменится целевая функция при изменении ресурса на единицу
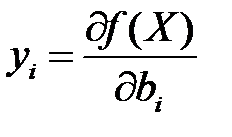 .
.
При малых приращениях 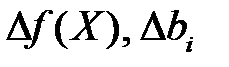 примем
примем 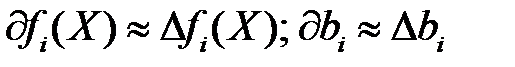 . Тогда
. Тогда 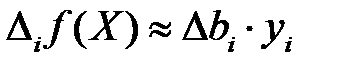 .
.
Полученное соотношение показывает, что при изменении 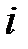 -го ресурса оптимальный доход является линейной функцией от приращения этого ресурса, причем коэффициентом данной функции является
-го ресурса оптимальный доход является линейной функцией от приращения этого ресурса, причем коэффициентом данной функции является 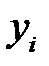 - i-я компонента решения двойственной задачи.
- i-я компонента решения двойственной задачи.
Если 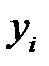 мало, то значительному приращению ресурса будет соответствовать незначительное увеличение оптимального дохода, т.е. ценность ресурса невелика.
мало, то значительному приращению ресурса будет соответствовать незначительное увеличение оптимального дохода, т.е. ценность ресурса невелика.
Если 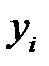 равно нулю, то при увеличении данного ресурса доход остается неизменным. Следовательно, ценность ресурса равна нулю. В самом деле, сырье, запасы которого превышают потребность в нем, не представляют ценности для производства и его оценку можно принять за ноль.
равно нулю, то при увеличении данного ресурса доход остается неизменным. Следовательно, ценность ресурса равна нулю. В самом деле, сырье, запасы которого превышают потребность в нем, не представляют ценности для производства и его оценку можно принять за ноль.
Если 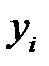 велико, то незначительному приращению ресурса будет соответствовать значительное увеличение оптимального дохода, т.е. ценность ресурса велика.
велико, то незначительному приращению ресурса будет соответствовать значительное увеличение оптимального дохода, т.е. ценность ресурса велика.
Следовательно, переменную 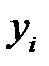 считают некоторой характеристикой ценности
считают некоторой характеристикой ценности 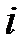 -го ресурса. В частности при увеличении данного ресурса на единицу, доход увеличивается на
-го ресурса. В частности при увеличении данного ресурса на единицу, доход увеличивается на 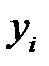 , что позволяет рассматривать
, что позволяет рассматривать 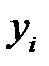 как условную цену, объективно обусловленную оценку
как условную цену, объективно обусловленную оценку  -го ресурса.
-го ресурса.
Так как 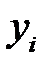 представляет собой частную производную оптимального дохода, то она характеризует скорость изменения оптимального дохода при изменении сырья.
представляет собой частную производную оптимального дохода, то она характеризует скорость изменения оптимального дохода при изменении сырья.
Предельные соотношения могут быть вычислены с помощью соотношений:
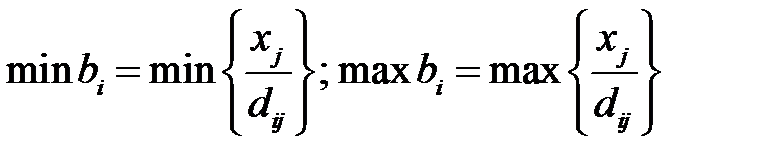 , где
, где 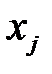 - значение переменной в оптимальном решении,
- значение переменной в оптимальном решении,  - элементы матрицы
- элементы матрицы 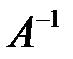 , обратной матрице базиса оптимального решения.
, обратной матрице базиса оптимального решения.
Чтобы оценить эффективность включения в оптимальный план новых видов продукции, используется следующая оценка
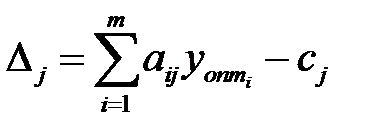 .
.
Если 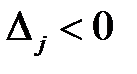 , то в план включаются новый вид продукции. Если
, то в план включаются новый вид продукции. Если 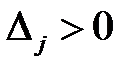 , то новый вид продукции водить нецелесообразно.
, то новый вид продукции водить нецелесообразно.
Пример.Пусть 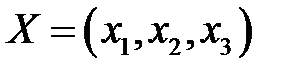 - план производства изделий трех видов. Задача линейного программирования сформулирована в виде
- план производства изделий трех видов. Задача линейного программирования сформулирована в виде
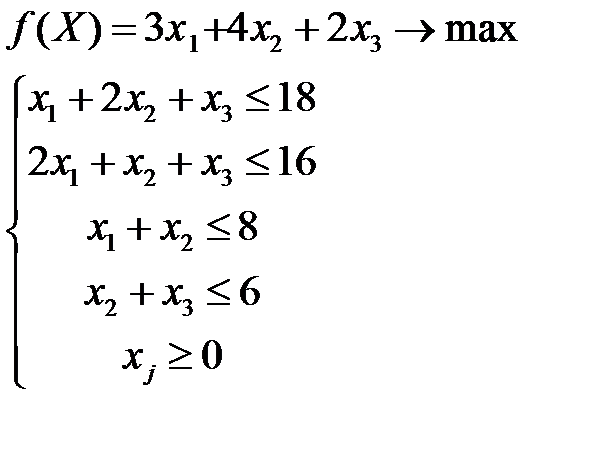
Предположим, что в результате решения задачи получен оптимальный план 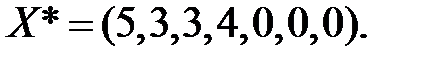
С помощью теорем двойственности найдено решение двойственной задачи 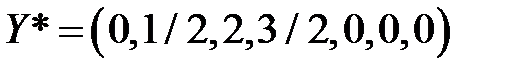 . Оптимальное значение целевой функции для обеих задач
. Оптимальное значение целевой функции для обеих задач 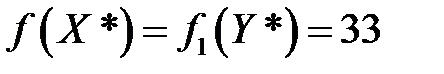 .
.
Видно, что наиболее дефицитным является третье сырье. Первое является недифицитным.
Для определения интервала устойчивости найдем обратную матрицу для базисных коэффициентов
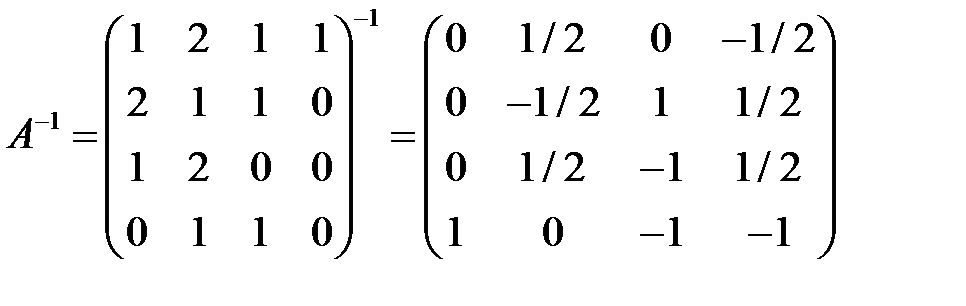 .
.
Интервал устойчивости определим для всех видов сырья
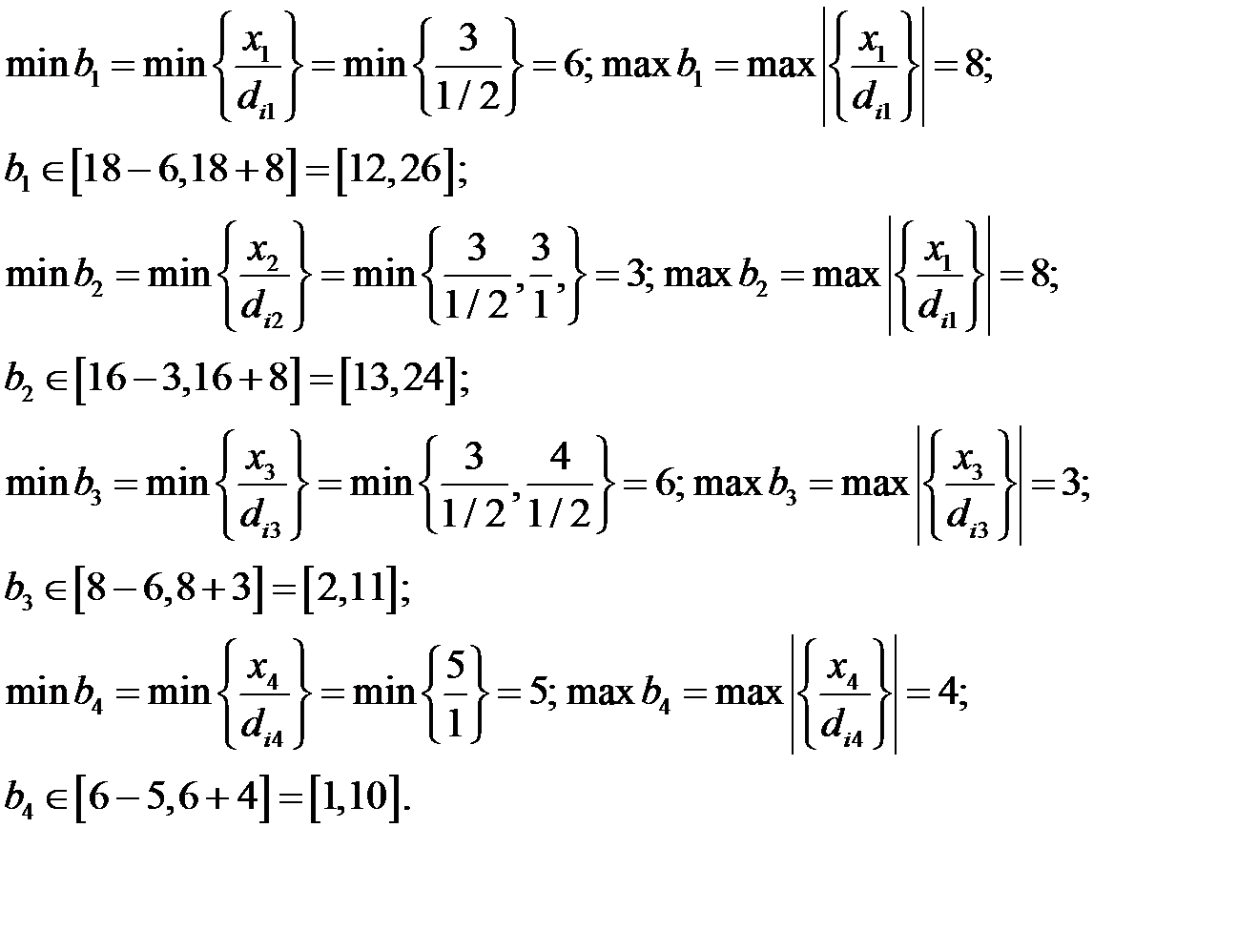
Определим целесообразность введения нового вида продукции. Если нормы затрат на данное сырье равны соответственно 1, 2, 2, 0, а доход составляет 15 ед.
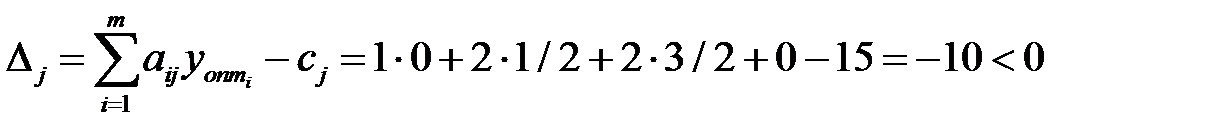 . Следовательно, новый вид товара вводить не целесообразно.
. Следовательно, новый вид товара вводить не целесообразно.
Дата добавления: 2016-05-28; просмотров: 9044;










