Ймовірнісні тести на простоту чисел.
Для скорочення кількості варіантів, які перевіряються детермінованими алгоритмами в деяких алгоритмах детермінованої групи використовуються ймовірнісні алгоритми.
На відміну від детермінованих тестів ймовірнісні тести перевірки простоти чисел побудовані з застосуванням випадкових чисел, відносно яких певні рівняння (умови) для простих чисел виконуються обов’язково, але можуть виконуватися для деяких не простих чисел. Тобто, якщо деяка умова не виконана, то число точно є складеним.
Якщо, навіть всі умови виконані, то стверджувати про простоту числа, яке тестується можна лише з певною вірогідністю. Цю ймовірність можна наблизити до 1, але це потребує збільшення кількості перевірок.
Звичайно, ці умови основані на малої теоремі Ферма, що стверджує, що для будь якого числа b>0, яке не перевищує деякого простого числа p виконується рівняння:
b(p–1)=1(mod p).
Наприклад, нехай p=11, оберемо b=2, тоді:
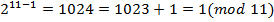 .
.
Таким чином, для з’ясування, чи є деяке число r простим, слід обрати будь яке додатне ціле число b<r, та перевірити виконання рівняння:
b(r–1)=1(mod r).
У випадку нерівності, число r відбраковується. В іншому випадку стверджують, що r – “псевдопросте по основанію b“. Ймовірність P(x) того, що складане число x з’явиться псевдопростим по випадковому основанію, зменшується з ростом x.
Наприклад, числа Кармайкла (зокрема, 561=3*11*17) можуть задовольнять вимозі теореми Ферма. Досі невідомо, скінченна або нескінченна множина чисел Кармайкла.
Тест Ферма можна суттєво посилити.
Визначення суворо псевдопростого числа. Нехай N – непарне число, N–1=d*2s, d – непарне. Число N називається суворо псевдопростим в базі a, якщо ad=1(modN) або
a(d*2r)=- 1(mod N) для деякого r: 0<r<s.
Ймовірнісний тест на простоту, заснований на перевірці на сувору псевдопростоту по випадковим називають тестом Селфриджа. Аналогів чисел Кармайкла (тобто чисел, суворо псевдопростих по всім базам, що не перевищують цього числа) в цьому випадку не має.
Оскільки тести, що базуються на теоремі Ферма, вимагають значного часу для обчислень, на практиці числа, які тестують, спочатку ділять на відносно маленькі прості числа. Якщо тестоване число поділено на одне з них, то воно завідомо не просте, якщо ж ні, то застосовується ймовірнісний тест.
Класичний результат теорії чисел – теорема Чебишева – свідчить, що частка додатних цілих чисел, які менше деякого цілого m та є простими, наближається до 1/(ln m). Наприклад, частка цілих простих чисел, менших 10100, близька до 1/(ln10100)=1/230. Оскільки 90% цих чисел лежать між 1099 та 10100, то частка простих чисел в цьому проміжку також складе величину біля 1/230.
Тому, якщо навмання обрати число з 99–ю десятковими цифрами, з ймовірністю біля 1/230 воно буде простим.
Дата добавления: 2016-06-15; просмотров: 1544;










