Детерміновані тести на простоту чисел

Методи перевірки чисел на простоту поділяють на дві основних групи: детерміновані та ймовірнісні. Кожна з зазначених груп методів має власні недоліки та переваги. Зокрема, у випадку застосування детермінованих методів висновок щодо простоти числа є остаточним, але процедура перевірки у обчислювальному плані є занадто складною та тривалою.

Застосування ймовірнісних методів дає можливість лише з певною надійністю вважати число простим, але відповідна обчислювальна процедура має придатні для практичних застосувань характеристики.

Простішим методом перевірки простоти натурального числа N є метод тестових ділень на число менше за N: d=2,3,4 … для перевірки виконання умови (d,N)>1. Очевидно, що максимальне 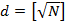– ціле число, яке не перевищує .

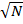У формалізованому вигляді цей метод отримав назву решета Ератосфена. Згідно цьому методу, для знаходження всіх простих чисел, що не перевищують заданого числа N, необхідно виконати наступні кроки:

1. Виписати всі цілі числа от двох до N:2,3,4, …, N.
2. Встановити початкове значення змінної p=2 ‑ першому простому числу.
3. Викреслити у списку числа от 2p до N рухаючиськроками шагами по p (це будуть числа кратні p: 2p, 3p, 4p, …).
4. Знайти перше не викреслене число в списку, яке більше ніж p, та встановити це число у якості нового значення змінної p.
5. Повторювати кроки 3 і 4, поки це можливо.

Якщо всі кроки виконані, то всі не викреслені числа в списку є простими числами від 2 до N.

На практиці, алгоритм Ератосфена можна покращити наступним чином. На кроці 3 можна викреслювати числа починаючи одразу с числа p², оскільки всі непрості числа що менше нього вже будуть викреслені. Та, відповідно, алгоритм зупиняється, коли p² перевищить N. Також, зважаючи на те, що всі прості 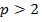‑ непарні числа, тому для них можна рухатися кроками по 2p, починаючи з p².

Складність (кількість операцій) T для цього методу оцінюється величиною :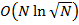

.

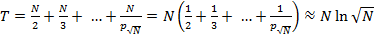Тут для оцінки часткової суми членів гармонійного ряду ми скористалися оцінкою Ейлера:

.

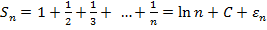Нагадаємо, що оцінка по порядку виду: 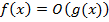, означає, що існує деяка константа C, для якої .

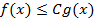Нескладно бачити, що кількість операцій, що потрібна для цього метода, так велика, що для чисел порядку 10³⁰…10⁴⁰ його складно застосувати.

Для ефективного застосування тесту решета необхідно деяким чином зменшити кількість чисел «кандидатів на простоту». Саме ця ідея закладена в основу цілої групи сучасних детермінованих тестів на простоту NFST (Number Field Sieve Tests).

Зокрема, класичний алгоритм групи NFST, що запропонований Адлеманом, Померансом та Румелі, використовуючи так звану китайську теорему про лишки, перевіряють простоту числа N за число кроків, яке для деякої константи c оцінюється величиною:

,

що значно краще ніж у випадку решета Ератосфена, але все ж такі ще досить складно.