Табличные интегралы
Интегралы, которые применяются для интегрирования элементарных функций и их комбинаций, называются табличными интегралами. Ниже приводятся основные табличные интегралы.
1.  , n Î R, n ¹ –1
, n Î R, n ¹ –1
2. 
3. 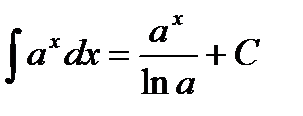
3а. 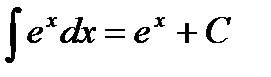
4. 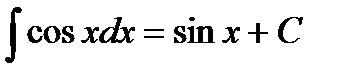
5. 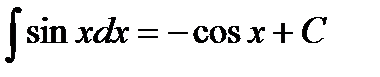
6. 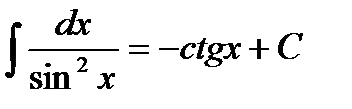
7. 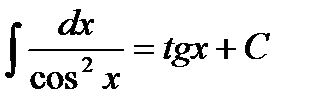
8. 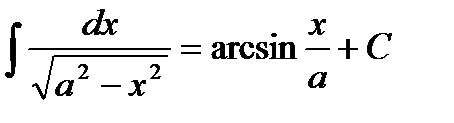
9. 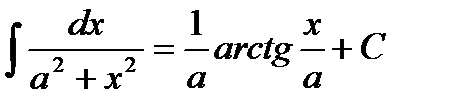
10. 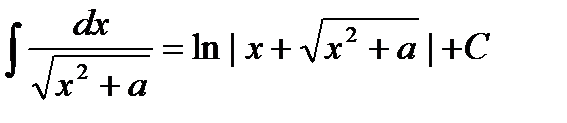
11. 
§4.3 Непосредственное интегрирование, интегрирование подстановкой, интегрирование по частям
Непосредственное интегрирование
Интегрирование называется непосредственным, если при интегрировании применяются только свойства интегралов и табличные интегралы.
@ Задача 1. Интегрировать функцию
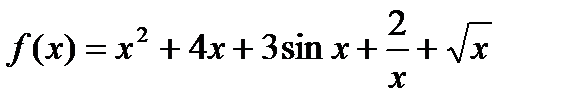 .
.
Решение: Интеграл вычисляется непосредственно с помощью свойств неопределенных интегралов и табличных интегралов:
.
Замечание: Нет нужды выписывать при промежуточных вычислениях для каждого интеграла свое постоянное слагаемое; достаточно приписать его по выполнения всех интегрирований.
Способ подстановки
Этот способ применяется, как правило, если подинтегральная функция сложная и нет возможности сразу брать интеграл с помощью табличных интегралов.
В подинтегральное выражение вместо x вводится вспомогательная переменная z, связанная с x некоторой зависимостью (как правило, аргумент подинтегральной сложной функции), после чего интеграл сводится к табличному интегралу.
@ Задача 2. Вычислить 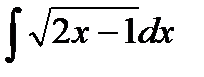 .
.
Решение: Производится замена переменных 2x – 1 = z, после чего 2x – 1 = z и dx = dz/2 подставляются в подинтегральное выражение, и интеграл сводится к табличному интегралу:
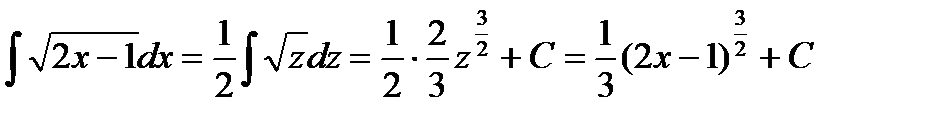 .
.
@ Задача 3. Вычислить 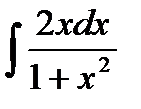 .
.
Решение: Производится замена переменных 1 + x2 = z, после чего находим 2xdx = dz. После подстановки получим:
 .
.
@ Задача 4. Вычислить 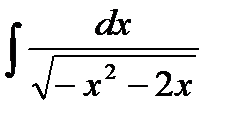 .
.
Решение: Под квадратным корнем, выделив полный квадрат, интеграл можно свести к табличному интегралу:
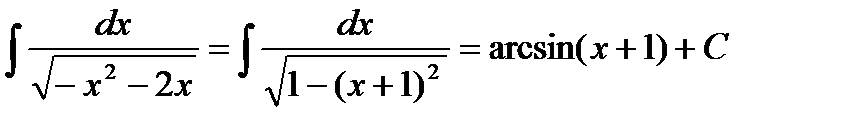 .
.
Дата добавления: 2016-06-15; просмотров: 4789;











