Характеристическая функция

Комплекснозначной случайной величиной называют функцию ξ₁(ω)+iξ₂(ω), где ωÎW, (ξ₁, ξ₂) – случайный вектор.

Например, 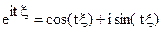– комплекснозначная случайная величина. По определению положим

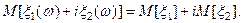(1)

Определение. Характеристической функцией φ_ξ(t) случайной величины ξ называется математическое ожидание комплекснозначной случайной величины 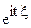, т.е.

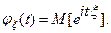(2)

Если f(x) - плотность распределения случайной величины ξ, то согласно определению

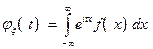(3)

Характеристическая функция определена для всех tÎ(-∞,∞) и удовлетворяет условию 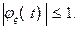Действительно,

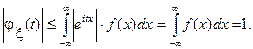
Из (3) видно, что характеристическая функция есть прямое преобразование Фурье плотности f(x). Воспользовавшись обратным преобразованием Фурье, получим в точках непрерывности плотности (см. §5 гл. 3 ).

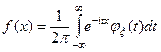. (4)

Из (4) следует, что если характеристические функции двух случайных величин совпадают, то совпадают и их плотности (законы) распределения. Точнее, они могут отличаться, но на множестве точек меры нуль.

Рассмотрим некоторые свойства характеристической функции.

1. Если η = aξ + b, то 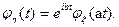Действительно, 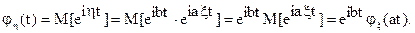Свойство доказано.

2. Характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций, т.е.

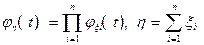
Действительно,

.

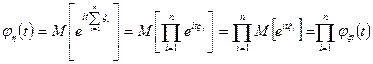Воспользовались теоремой о математическом ожидании от произведения независимых случайных величин (см. §20).

3. Если абсолютный начальный момент n-го порядка существует, т.е. 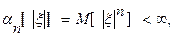то характеристическая функция φ_ξ(t) дифференцируема n раз, причем

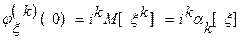, k = 0,1,…,n. (5)

Доказательство. Продифференцируем (3) k раз по t и убедимся, что полученный интеграл сходится.

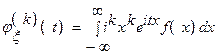. (6)

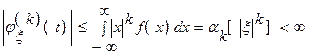по условию.

Следовательно, дифференцирование законно. Из (6) при t=0 получим (5). Свойство доказано.

Разложим φ_ξ(t) в ряд Тейлора в окрестности точки t=0, ограничившись тремя членами разложения

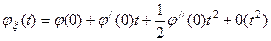. Согласно (5) φ(0)=1, φ^/(0)= iα₁ = im_ξ, φ^//(0)= i²α₂ = -(D_ξ+m_ξ²). Итак,

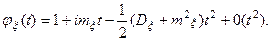(7)

Рассмотрим случайную величину ξ с математическим ожиданием m_ξ= 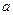и дисперсией D_ξ=σ². Случайная величина

ξ* = (ξ– 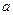)/σ (8)

называется нормированной. Легко проверить, что M[ξ*]=0, D[ξ*]=1. Пусть ξ* распределена по стандартному нормальному закону, тогда ее плотность распределения 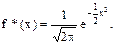Найдем ее характеристическую функцию. Согласно (3)

=

= =

= .

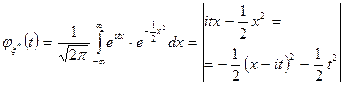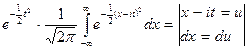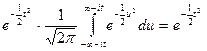Мы воспользовались тем, что 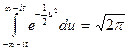. Итак,

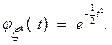(9)

Из (8) найдем ξ=σξ*+ 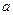. По свойству (1) и с учетом (9) получим характеристическую функцию случайной величины ξ.

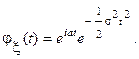(10)

Докажем, что (10) есть характеристическая функция нормального распределения N( 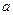,σ). Действительно, по формуле (4)

.

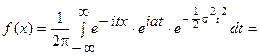
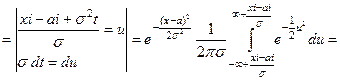
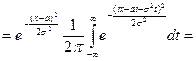
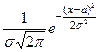Итак, 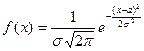. (11)

Формула (11) доказывает наше утверждение. Таким образом, если случайная величина ξ распределена по нормальному закону N( 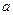,σ), то нормированная величина ξ* распределена по стандартному нормальному закону N(0,1).