Подобие треугольников в курсе геометрии 8 класса.
Цели изучения:
· сформировать понятие подобных треугольников;
· изучить признаки подобия треугольников;
· рассмотреть применение подобия к доказательству теорем и решению задач.
Содержание учебного материала по учебнику Л.С. Атанасяна
«Геометрия. 7 - 9 классы».
Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
При этом если у треугольников АВС и А1В1С1 углы соответственно равны: ÐА = ÐА1, ÐВ = ÐВ1, ÐС = ÐС1, то стороны АВ и А1В1, ВС и В1С1, АС и А1С1 называют сходственными.
Другими словами, два треугольника подобны, если для них можно ввести обозначения АВС и А1В1С1 так, что ÐА = ÐА1, ÐВ = ÐВ1, ÐС = ÐС1 (1),
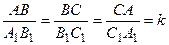 . Число k, равное отношению сходственных сторон, называется коэффициентом подобия.
. Число k, равное отношению сходственных сторон, называется коэффициентом подобия.
Вводится обозначение DАВС ~ D А1В1С1.
Далее изучаются признаки подобия треугольников.
Первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство первого признака основывается на теореме, доказанной ранее: если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы (с. 126).
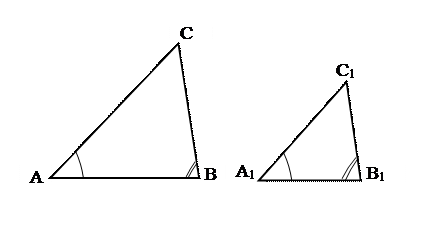 Дано: АВС и А1В1С1
Дано: АВС и А1В1С1
ÐА = ÐА1, ÐВ = ÐВ1
Доказать:
DАВС ~ D А1В1С1
Доказательство.
1. ÐС=180°-ÐА-ÐВ.
ÐС1=180°-ÐА1-ÐВ1.
ÐС = ÐС1, следовательно, углы треугольника АВС равны соответственно углам треугольника А1В1С1.
2. Так как ÐА = ÐА1, ÐС = ÐС1, то 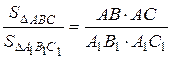 и
и 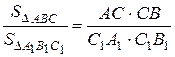 .
.
Из этих равенств следует, что 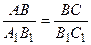 . Аналогично, используя равенства
. Аналогично, используя равенства
ÐА = ÐА1 и ÐВ = ÐВ1, получаем 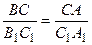 . Пропорциональность сходственных сторон треугольников доказана. Итак, DАВС ~ D А1В1С1.
. Пропорциональность сходственных сторон треугольников доказана. Итак, DАВС ~ D А1В1С1.
Второй признак подобия треугольников:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами равны, то такие треугольники подобны.
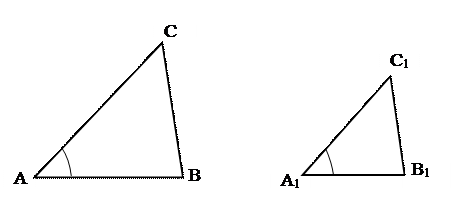
Дано: АВС и А1В1С1
ÐА = ÐА1, 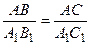 .
.
Доказать:
DАВС ~ D А1В1С1
Доказательство
Доказательство второго признака сводится к первому признаку: достаточно доказать, что ÐВ = ÐВ1.
1. Рассмотрим треугольник АВС2: Ð1 = ÐА1, Ð2 = ÐВ1.
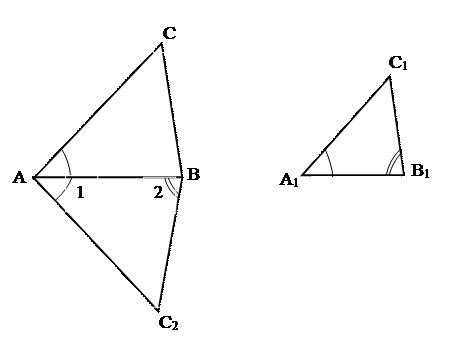
DАВС2 ~ DА1В1С1 (по двум углам), поэтому 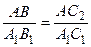 . По условию
. По условию 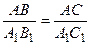 , следовательно, АС=АС2.
, следовательно, АС=АС2.
2. DАВС = DАВС2 (по двум сторонам и углу между ними). Следовательно,
Ð2 =ÐВ и Ð2 =ÐВ1: ÐВ = ÐВ1. Тогда DАВС ~ D А1В1С1 (по двум углам).
Третий признак подобия треугольников: если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Доказательство третьего признака сводится ко второму признаку и аналогично ему. Рассмотреть самостоятельно (с. 144).
В учебнике рассматриваются практические приложения подобия треугольников: при решении задач на построение методом подобия и при проведении различных измерительных работ на местности (определение высоты предмета и расстояния до недоступной точки).
Содержание учебного материала по учебнику А.В. Погорелова
«Геометрия. 7 - 11 классы».
Определение. Две фигуры называются подобными, если они переводятся друг в друга преобразованием подобия. Обозначение F~F¢.
Таким образом, два треугольника называются подобными, если они переводятся друг в друга преобразованием подобия.
Напомним, что преобразование фигуры F в фигуру F¢ называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Это значит, что если произвольные точки X, Y фигуры F при преобразовании подобия переходят в точки Х¢, Y¢ фигуры F¢, то Х¢ Y¢ =k×X Y. Причём число k - одно и то же для всех точек X, Y. Число k называется коэффициентом подобия.
Рассматриваются свойства преобразования подобия, в частности, оно сохраняет углы между полупрямыми.
Рассматривается преобразование гомотетия, которое задаётся центром и коэффициентом гомотетии – положительным числом k.
 Построим точку Х¢, гомотетичную точке Х. Для этого проведем луч Ох и на нём отложим отрезок ОХ¢=2ОХ. Аналогично строится точка Y¢, гомотетичная точке Y.
Построим точку Х¢, гомотетичную точке Х. Для этого проведем луч Ох и на нём отложим отрезок ОХ¢=2ОХ. Аналогично строится точка Y¢, гомотетичная точке Y.
Преобразование фигуры F, при котором каждая её точка Х переходит в точку Х¢, построенную указанным способом называется гомотетией относительно центра О. Фигуры F и F¢ называют гомотетичными.
Доказывается, что гомотетия есть преобразование подобия.
Из свойств преобразования подобия следует, что у подобных треугольников DАВС и D А1В1С1 ÐА = ÐА1, ÐВ = ÐВ1, ÐС = ÐС1 и 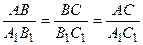 .
.
Дата добавления: 2016-06-15; просмотров: 3424;










