Потери при нескольких временах релаксации

Обобщим формулы для ε' и ε" на случай набора времен релаксации. Пусть f(τ) — относительная вероятность, что время релаксации равно τ. Если у всех молекул одно и то же τ, эта вероятность равна единице. При наборе времен релаксации f(τ)dτ есть вероятность того, что время релаксации лежит в интервале от τ до τ+dτ, причем

.

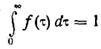Интегрирование выполняется от нуля до бесконечности, так как время релаксации должно иметь какое-либо значение в этих пределах. Если же нет времен релаксации, меньших τ_a и больших τ_b, то в интеграле можно было бы в качестве пределов интегрирования взять τ_a и τ_b. Значение интеграла не изменилось бы, так как интеграл от нуля до τ_a и от τ_b до бесконечности был бы равен нулю вследствие равенства нулю вероятности f(τ) при τ < τ_a и τ > τ_b. Поэтому, принимая в качестве пределов интегрирования нуль и бесконечность, мы не изменяем значение интеграла. При учете распределения времен релаксации [см. ] выражения для ε' и ε" изменятся и запишутся следующим образом:

,

.

В случае одного времени релаксации эти формулы принимают вид выражений .

Функцию распределения можно подобрать так, чтобы вычисленные значения соответствовали экспериментальным данным, однако при этом функция распределения может иметь сложный вид. Простые функции распределения, в частности функция распределения Гаусса, приводят к сложным зависимостям ε' и ε" от частоты, которые в некоторых случаях относительно хорошо совпадают с экспериментальными данными.

При выборе функции распределения f(τ) необходимо учитывать, что одновременно с расширением максимума в частотном ходе ε" или tgδ происходит уменьшение максимальных значений ε" и tgδ. Вследствие этого площадь S, ограниченная кривой, изображающей зависимость ε" от ln ω, и осью абсцисс, на которой отложен ln ω, не зависит от конкретного вида правильно выбранной функции распределения f(τ). На Рис. 7‑8 эта площадь заштрихована.

Рис. 7‑8. К определению функции распределения времен релаксации f (τ), которая выбирается так, чтобы заштрихованная площадь равнялась

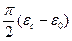
Вычислим площадь

.

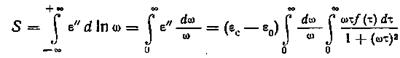Здесь использована формула для ε" и принято во внимание, что 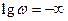при ω == 0. Меняя в порядок интегрирования, находим

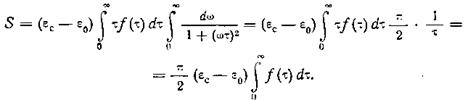
Так как 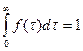, то

.

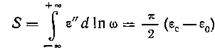Условие учитывается при выборе вида выражения для ε", правильно описывающего зависимость ε" от частоты в случае, когда имеется распределение времен релаксации.

7.7.3. Рассмотрим одно из выражений для ε", предложенное Фуоссом и Кирквудом. Перепишем в виде

.

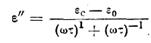Когда ωτ == 1, ε" принимает значение

.

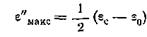Значение ε" в максимуме можно уменьшить, умножив правые части выражений и на λ, где 0 < λ < 1.

Выражение для ε" Фуосс и Кирквуд записывают в виде

,

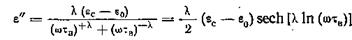здесь τ_в - наиболее вероятное время релаксации, вокруг которого группируются времена релаксации молекул,
0 < λ < 1 дает более широкий и менее высокий максимум, чем формула .

Величина ε" в максимуме при ωτ_в == 1 равна

.

Чем меньше λ, тем слабее зависимость ε" от ω, тем шире максимум в частотном ходе ε" и тем более широкая функция распределения времен релаксации f(τ). Как легко проверить, функция Фуосса и Кирквуда удовлетворяет условию .