Класс моделей полигональных объектов

Полигональный объект (полигон) в векторном формате пространственных данных определяется через замкнутую полилинию, которая представляет собой границу части территории, имеющую определенные свойства. Следовательно, описание полигона V_j совпадает с описанием полилинии L_j (49). Отличие в данном случае заключается в замкнутости L_j, т.е. первый и последний узлы совпадают.

Свойства данной части территории (полигонального объекта) будем определять как множество сгруппированных узловых точек сети участков, имеющих один и тот же коэффициент веса:

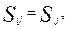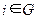для , (44)

где G – множество узловых точек ЭУ w_i, находящихся на территории, ограниченной полилинией – границей полигона.

Выражение (44) дает следующий алгоритм построения модели полигонального объекта. Необходимо определить, лежит ли текущая i-я точка внутри j-го полигонального объектаV_j, представляющего собой участок территории, ограниченный замкнутой полилинией L_j. Если да, то S_ij ® S_j, иначе S_ij ® 0 (см. также выражение (25).

Сложность реализации данного алгоритма обусловлена необходимостью решения топологической задачи по определению принадлежности текущей точки полигональному объекту. Возможно несколько способов решения данной задачи. Рассмотрим два наиболее перспективных.

Суть первого способа заключается в следующем (рис. 26):

1. Вычисляется площадь исходного полигона V_j.

2. На основе исходного полигона строится новый, границы которого представляют собой полилинию, проходящую через все исходные узлы и текущую P_i точку.

3. Вычисляется площадь полученного полигона V_jp.

4. Если V_jp > V_j, то точка P_i лежит вне полигона,

если V_jp£ V_j, то точка P_i принадлежит полигону V_j.

Реализация этого способа связана с построением нового полигона и вычислением площади фигуры произвольной формы, что при невыпуклых конфигурациях полигонов делает необходимым решение нетривиальной задачи выбора узлов для такого построения.

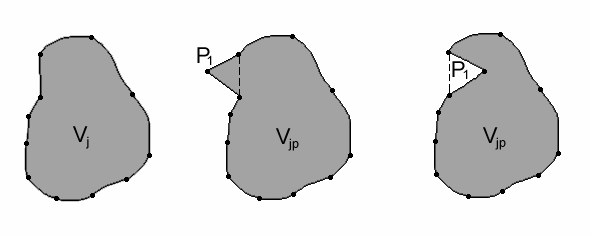
Рис. 26. Определение принадлежности текущей точки полигональному объекту (первый способ)

Второй способ выглядит более перспективным. Его идея заключается в определении числа пересечений m луча произвольного направления из точки P_i с линией границы полигона. Алгоритм следующий:

1. Если m – четное число, то P_i лежит вне полигона V_j.

2. Если m – нечетное, то P_i принадлежит полигону V_j.

Из рис. 27 видно, что это справедливо для любой формы полигона, в том числе и квазикольцеобразной формы.

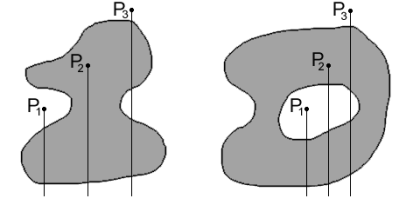
Рис. 27. Определение принадлежности текущей точки полигональному объекту (второй способ)

Наиболее просто задача решается, если лучи опускать перпендикулярно. Последовательность операций при решении топологической задачи принадлежности точки P_i полигону V_j заключается в следующем:

1. Определить, является ли полилиния L_j замкнутой; если да, то объект – полигон.

2. Исключить из рассмотрения отрезки l_jn полилинии L_j, которые лежат выше точки P_i.

3. Определить для оставшихся отрезков, лежит или нет точка P_i на одном из них; если да, то P_i принадлежит V_j.

4. При несоблюдении условия из п. 3 определяется количество пересечений m вертикали, проходящей через точку P_i, с отрезками полилинииL_j, лежащими ниже точки P_i. Если число m – нечетное, то P_i принадлежит V_{j .}

Кроме того, необходимо выделить предельные случаи, когда вертикальный луч проходит через узел, т.к. вопрос четного или нечетного пересечения сходящихся в этом узле отрезков является неопределенным. На рис. 28 представлены типичные примеры взаимного положения полигона V_j, заданного замкнутой полилинией в виде списка узловых точек P₁–P₁₀, и текущих точек рассматриваемой территории P₁₃–P₁₇. Реализацию алгоритма принадлежности текущих точек полигону V_j целесообразно осуществлять так же, как и при построении модели влияния полилинии с последовательного определения взаимного положения отрезков l_jn и точек P_i.

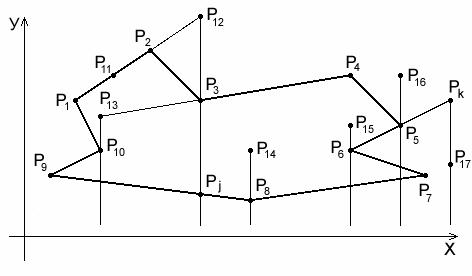
Рис. 28. Типичные примеры взаимного положения полигона Vj, заданного
замкнутой полилинией в виде списка узловых точек P₁–P₁₀ и точек P₁₃–P₁₇

При этом в первую очередь определяется, лежит ли текущая точка на границе полигона, т.е. на отрезке l_jn. Вычисляется коэффициент наклона отрезков l_jn и линии, соединяющей текущую точку с одной из вершин по выражению (53). Если, например, для отрезка l₁₂

k_l=k_n+1 и (X₃–X₁)(X₃–X₂)<0,

или в общем виде

(X_i–X_n)(X_i–X_n+1)<0, (45)

то точка P_i лежит на отрезке l_n,n+1 (P₃ на l₁₂) и принадлежит V_j.

Если условие (45) не соблюдается, то вопрос о принадлежности остается открытым. Например, P₁₂ не принадлежит V_j, а точка P₁₃, лежащая на продолжении линии l₃₄, принадлежит V_j. Для определения принадлежности, как было показано выше, необходимо подсчитать количество пересечений m вертикального луча из P_i с отрезками полилинии L_j. При реализации данного этапа алгоритма определяется, проходит ли вертикаль, опущенная из текущей точки, через узел полилинии L_j, или нет. Если проходит, т.е. X_i=X_n, например, для точки P₁₂ X₁₂=X₄ и для точки P₁₃ X₁₃=X₁₀, то необходимо определить, рассматривать ли это пересечение, или нет. Из рис. 28 видно, что когда отрезки сходятся в узел с разных сторон вертикали (точки P₁₂, P₁₄), то пересечение с такими узлами (P₃, P₈) необходимо учитывать (т.е. m®m +1).

В том случае, когда отрезки лежат по одну сторону от вертикали (точки P₁₃, P₁₅, P₁₆), то пересечения с их узлами (P₁₀, P₆, P₅) необходимо отбросить при подсчете общего числа пересечений, т.е. m®m. Признак такого взаимоположения, например, отрезков l₅₆, l₆₇ и вертикали из точки P₁₅ дает выражение (X₅–X₁₅)(X₇–X₁₅)>0.

В общем виде:

если (X_n–X_i) (X_n+2–X_i)<0, то m®m+1

если (X_n–X_i)(X_n+2–X_i)>0, то m®m.

И, наконец, рассмотрим наиболее часто встречающийся случай определения пересечения вертикали с отрезками полилинии L_j (например, (см. рис. 28) для точек P₁₂, P₁₃ пересечение с l₆₇, для P₁₆ пересечение с l₆₇ и l₇₈). В начале определяется координата Y точки пересечения P_j с отрезком l_n,n+1 и вертикалью из точки P_i:

.

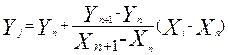Затем определяется, лежит ли точка пересечения ниже текущей точки путем сравнения их координат: Y_j < Y_i. Если да (это условие совпадения), то определяется, пересекает ли вертикаль отрезок l_n,n+1. Признак пересечения определяет выполнение условия:

если (X_i–X_n) (X_i–X_n+1)< 0, то m®m +1, иначе m®m.

Эти операции включают в себя процедуру проверки: расположен ли отрезок полилинии выше или ниже точки P_i. На рис. 28 показан для примера случай определения взаимоположения точки P₁₇ и лежащего выше отрезка l₅₆. Для точки пересечения P_k вертикали с линией, являющейся продолжением этого отрезка, справедливо выражение:

.

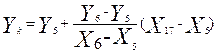Так как Y_k > Y₁₇ , то точка пересечения игнорируется.

Полный последовательный перебор всего множества отрезков l_jn даст исчерпывающую картину взаимного положения текущей точки территории P_i и полигона V_j. Рассмотрение всех текущих точек P_i, где iÎI, даст, в свою очередь, полную структурно-позиционную модель пространственного влияния полигонального объекта.

Наиболее часто встречается на практике модель, отражающая, например, занятость конкретного участка территории каким-либо зданием или сооружением, физические свойства грунта, как в рассмотренном в гл. II примере, и т.д. Однако имеется значительное количество полигональных объектов, пространственное влияние которых не ограничивается размерами этого объекта. Например, влияние на экологическую обстановку зеленого массива. Модель таких объектов будет представлять собой комбинацию модели полигона (44) и линейной модели (41) для точек, лежащих вне полигона. Алгоритм получения такой модели, очевидно, будет представлять комбинацию алгоритмов для полигона и полилинии. На рис. 29 представлена иерархическая система класса моделей полигональных объектов.

Простая модель без функции внешнего влияния

Простая модель с симметричным Простая модель с асимметричным

законом влияния законом влияния

Рис. 29. Класс моделей пространственного влияния полигональных объектов

Она построена по принципу «от простого к сложному», когда последующая модель является модификацией (наследницей) моделей, находящихся на предыдущем уровне.

Рассмотренный способ получения позиционного описания свойств территории не накладывает ограничения на величину w_i. Однако с уменьшением размеров w_i в квадратичной зависимости растет количество точек r_i, а, следовательно, и объем расчетных задач. Поэтому определение оптимальных размеров ЭУ является самостоятельной задачей.

§ 3. Методы определения величины квантования модели
исследуемой территории

В первом приближении величина ЭУ (ячеек) может быть определена на основе размеров исследуемой территории и требуемой точности моделирования

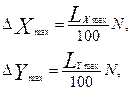(46)

где L_Xmax и L_Ymax – максимальный размер территории по соответствующим координатам, N – требуемая точность разбивки территории, %.

Для нахождения оптимального значения величин DX и DY используем спектральный метод. Представим функцию f_V(r) в виде спектра пространственных («застывших») волн, расходящихся от объекта на прилегающую территорию.

Проблему представления непрерывного рельефа в численно-матричном виде без потери полезной информации, т.е. определения оптимального периода квантования (в нашем случае величины шага сетки), можно решить использованием теоремы Котельникова.

Согласно теореме любой непрерывный процесс с ограниченным спектром может быть полностью описан дискретной последовательностью его мгновенных значений, следующих с частотой, как минимум вдвое превышающей частоту наивысшей гармоники процесса. Частота выборки мгновенных значений (отсчетов) называется частотой дискретизации (квантования). Она должна быть больше 2f_max, где f_max– максимальная присутствующая в спектре сигнала частота (частота среза).

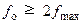, (47)

где f_о– оптимальная частота квантования по времени; f_max – частота среза.

Выражение (47) применяется для временных рядов. В данном случае изменение функции происходит в пространстве, а не во времени. Поэтому проводится замена обозначения используемых переменных: f (временная частота) на φ (пространственная частота); Т (период) на L (длина отрезка повторения функции); 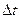(шаг измерения во времени) на 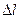(шаг измерения в пространстве). Таким образом, выражение (47) трансформируется в

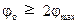(48)

где φ_о – оптимальная частота квантования в пространстве; φ_max – частота среза.

Если представить 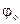(w) в показательной форме относительно длины волны 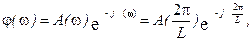(49)

тогда выражение 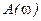, учитывая, что 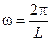, будет представлять величины амплитуд пространственных волн для конкретных значений .

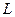Задав минимальное значение амплитуды A_min(w_max) из выражения (49),например, 0,01 от максимального значения функции пространственного влияния, получим минимальное значение длины волны 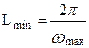, которую необходимо учитывать при моделировании. Тогда по теореме Котельникова – Шенона максимальное расстояние между текущими точками, определяется следующим выражением:

.

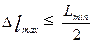То есть размеры DX_min и DY_min ЭУ w_i, на которые разбивается исследуемая территория, должны равняться .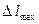

Как правило, на практике используют частоту, превышающую частоту Котельникова в 2–5 раз.

Проделав элементарные преобразования, получим, что для повторяющихся (в классическом случае – периодических) функций наибольшим периодом квантования является половина длины волны гармоники с наибольшей частотой. Исходя из этого и найдя гармоническую составляющую с наименьшей длиной волны, можно определить оптимальный шаг задания функции.

Исключение из спектра функции составляющих с небольшой амплитудой позволяет добиться увеличения шага квантования при несущественных потерях информации.

Для решения поставленных проблем используем математический аппарат спектрального анализа функции, трансформировав его также из временной области в пространственную.

Сущность гармонического анализа заключается в представлении функций в виде суммы гармонических колебаний. Классический гармонический анализ состоит в разложении периодических функций в сходящийся ряд Фурье. В нашем случае обрабатывается непериодическая (финитная) функция, т.е. ряд функций, полностью определенных на отрезке [0, l₀].

Функция Y(x)раскладывается в ряд вида:

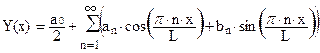; (50)

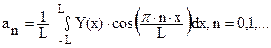; (51)

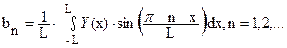, (52)

где a_nи b_nназывают коэффициентами Фурье.

В большинстве случаев, например, когда анализируемая функция задана сложным аналитическим выражением, таблицей или графиком, для определения коэффициентов ряда используются либо численные методы, основанные на квадратурных формулах, либо графические приемы, либо специальные приборы (гармонические анализаторы). В этом случае используем разложение в ряд следующего вида:

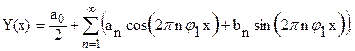(53)

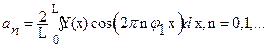; (54)

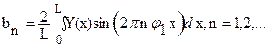, (55)

где L – отрезок повторения функции, 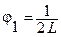– частота повторения (или частота первой гармоники), n – номер гармоники.

В формулах (69, 70, 71) диапазон повторения функции составлял 2L, а в формулах (72, 73, 74) – 1L.

Спектром функциональной зависимости Y(x) называется совокупность ее гармонических составляющих (гармоник), образующих ряд Фурье. Спектральный анализ повторяющихся функций заключается в нахождении коэффициентов a_n и b_n ряда Фурье.

Обобщенный спектральный анализ базируется на том, что повторяющиеся функции Y(x) являются частными случаями финитных функций. Действительно, полагая l₀= L (этим мы условно приписываем финитным функциям диапазон изменения L) и считая 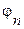= n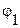(при финитных функциях n – любые, а при периодических – целые числа), получаем:

;

.

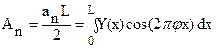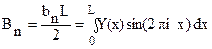Численный спектральный анализ заключается в нахождении коэффициентов a₀,..., a_n, b₁,...,b_n для повторяющейся (периодической) функции у(х), заданный на отрезке [0, L] дискретными отсчетами.

При применении численных методов коэффициенты A_n и B_n будут находиться следующим образом:

;

.

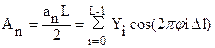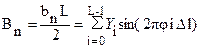Аппарат гармонического анализа применяется к функции одной переменной. Применительно к пространственно распределенной информации (в нашем случае она представлена в виде функции двух переменных) необходимо адаптировать методику. Возможны различные варианта приведения функции двух переменных к функции одной переменной.

«Строчный» метод заключается в преобразовании трехмерного рельефа к непрерывной линии путем свертки участков, когда вслед за последним значением i-го участка считывается последнее значение i+1 участка. Движение считывания: слева направо, затем справа налево. Кроме того, задается некоторое значение величины в процентах от максимальной амплитуды и отбрасываются гармоники с меньшим значением амплитуды.

«Последовательный» метод заключается в преобразовании трехмерного рельефа к непрерывной линии путем свертки участков, когда вслед за последним значением i-го участка считывается первое значение i+1 участка. Движение считывания всегда проходит слева направо.

§ 4. Интерполяция пространственных моделей

Квантование исследуемой территории максимально допустимыми по размерам ЭУ в значительной степени ускоряет процессы пространственного анализа и моделирования. Однако это приводит к тому, что получаемая модель свойств территории будет представляться статистической поверхностью (рельефом), имеющей ступенчатый вид. Для сглаживания этой поверхности необходимо применить интерполяцию, т.е. сглаживание рельефа за счет вычисления промежуточных точек между уже имеющимися. Получаем рельеф, хотя и рассчитанный по разреженной системе точек, принадлежащих ЭУ, но имеющий близкий к непрерывной поверхности вид. Такой рельеф будет более информативен в том случае, если интерполяция осуществлена методом, обеспечивающим представление объектов или поверхностей между имеющимися точками близко к реальному виду. Интерполяция наиболее эффективна тогда, когда известно, что между имеющимися расчетными точками объектов нет резких изменений, т.е. наблюдается плавный переход. Технология определения размеров ЭУ, описанная в § 2 данной главы, как раз и обеспечивает выполнение этого условия.

Наиболее эффективным для интерполяции в рассматриваемых случаях является использование сплайнов. Методы, основанные на сплайнах, заняли прочное место среди наиболее мощных средств вычислительной математики. В настоящее время они стали общепринятым не только среди специалистов по теории приближения и вычислительной математики, но и среди инженеров, связанных с решением прикладных задач на ЭВМ. Популярность сплайнов объясняется в основном двумя причинами.

Во-первых, сплайны представляют собой чрезвычайно мощное и гибкое средство решения разнообразных задач приближения функций. Эти задачи, помимо их самостоятельного значения, лежат в основе многих методов вычислительной математики.

Во-вторых, математический аппарат, используемый для данного вида интерполяции, хорошо проработан и широко освещен в специальной литературе [23, 24].

В-третьих, алгоритмы, построенные с помощью сплайнов, эффективно реализуются на ЭВМ.

По сравнению с другими интерполяционными полиномами сплайн-функция отвечает следующим условиям:

1. Функция F(x) непрерывна на исследуемом отрезке[a,b]вместе со своими производными F'(x), F''(x),..., F^(p) (x) до некоторого порядкаp.

2. На каждом отрезке [x_i-1, x_i] функция F(x) совпадает с некоторым многочленом степени m.

Наиболее распространены кубические сплайны, которые эффективны и в рассматриваемом случае. При этом получаются непрерывными и функция, и ее производные до второго порядка включительно.

Технология интерполяции кубическими сплайнами следующая. Интерполяционный кубический сплайн F(x) состоит из отдельных сегментов F₀(x), F₁(x), ..., F_n-1(x), каждый из которых определен на соответствующем отрезке, т.е. сегмент F_i(x) относится к отрезку [x_i, x_i+1]. Функции F_i(x) являются многочленами 3-й степени

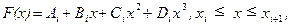
гдеi = 0, 1,…, n-1, так что в целом сплайн-функция F(x) содержит 4n коэффициентов A_i, B_i, C_i, D_i.

Методики вычисления коэффициентов весьма разнообразны, но при любых обстоятельствах они отвечают условиям, указанным выше в данном параграфе. В нашем случае использовались следующие выражения:

,

,

,

.

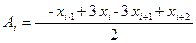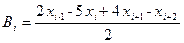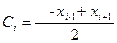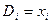Технология и результаты применения интерполяции показаны на рис. 29. Как видно из рис. 29, после применения интерполяции, представление исходной поверхности в графическом виде несколько трансформировалась, теперь она стала более сглаженной. Это проявилось в том, что изменились вид и границы эквидистантных линий.

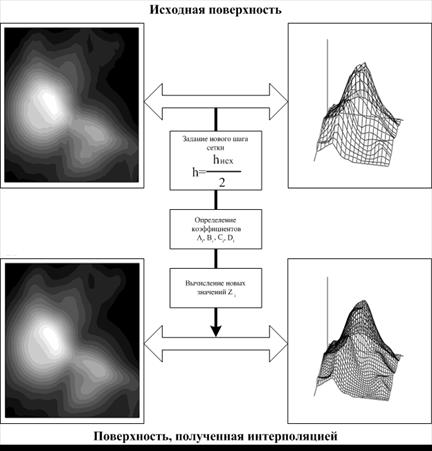
Рис. 29. Интерполяция поверхности бикубическими сплайнами

Таким образом, применение интерполяции бикубическими сплайнами позволяет привести все используемые модели тематических слоев к одному минимальному шагу задания сетки.

§ 5. Фильтрация пространственных моделей

Свойства территории, получаемые с помощью функций пространственного влияния объектов, хранится в памяти компьютера в виде двумерного массива чисел, в котором каждое число определяет свойство территории в соответствующем ЭУ. При проведении анализа этих свойств необходимо убрать незначительные изменения этих свойств (отфильтровать шумы) и выявить зоны особых «всплесков», например, резких изменений свойств территории. Для этого необходимо осуществить фильтрацию получаемого в результате моделирования числового двумерного массива.

Фильтрация поверхности имеет много общего с хорошо известной в радиотехнике фильтрацией сигналов. Отличие состоит в том, что вместо «одномерного» фильтра, предназначенного для фильтрации зашумленного сигнала одной переменной (обычно – времени), для фильтрации поверхности применяются двумерные фильтры, которые представляют собой прямоугольный участок плоскости (апертуру), состоящий из ЭУ с определенными весовыми коэффициентами (коэффициентами фильтрации). Процедура фильтрации состоит в том, что данная апертура (двумерный фильтр) накладывается на фильтруемую поверхность (двумерный массив чисел свойств территории), и численные значения соответствующего ЭУ умножаются на весовой коэффициент совпадающего ЭУ апертуры. Затем полученные произведения суммируются и делятся на число ЭУ фильтра. Это среднеарифметическое значение присваивается центральному ЭУ. Фильтрация всей территории (всего массива) осуществляется путем перемещения апертуры по поверхности. В каждом положении апертуры выполняются однотипные действия, которые и определяют отклик фильтра. Данный тип фильтрации относят к пространственно-инвариантным операциям. Апертура вместе с заданной на ней весовой функцией часто называется маской [25].

Минимальный размер апертуры равен 3´3. Он обеспечивает локальную фильтрацию. Увеличение размера апертуры усиливает действие фильтра, но при этом может произойти существенное искажение информации. Это обусловлено тем, что если размер числового массива много больше размера апертуры (окна), то доля площади профильтрованного поля, на которой заметны краевые эффекты, очень мала.

Рассматриваемый механизм позволяет реализовать следующие группы фильтров: низкочастотные, высокочастотные, операторы Лапласа, курсовые градиентные.

Рассмотрим подробнее каждую из них.

Низкочастотные фильтры применяются для отсечения из спектра высокочастотных составляющих, что позволяет исключить из временного ряда или, как в нашем случае, пространственного изображения, пиковые всплески малой площади.

На рис. 30 представлены результаты работы группы низкочастотных фильтров, имеющих следующие маски:

Фильтр 1: 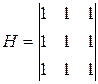; Фильтр 2: ;

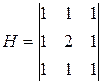Фильтр 3: 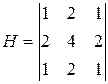; Фильтр 4: .

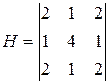На исходной модели буквами обозначены зоны, которые не несут практически значимой информации. Все предложенные фильтры «справились» с поставленной задачей. Необходимость введения в систему нескольких однотипных фильтров объясняется тем, что помимо исследуемых зон фильтр также затрагивает и оставшиеся участки, изменяя их значения в большей или меньшей степени, в зависимости от маски.

Высокочастотные фильтры по своему функциональному предназначению составляют противоположность предыдущей группе. В этом случае значения на участках модели после фильтрации выделяются увеличением их амплитуды. Степень интенсивности изменения определяется выбранной маской.

б

в

а

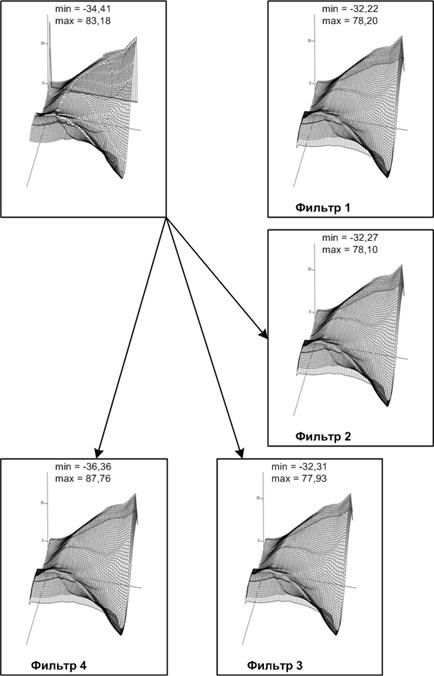
Рис. 30. Обработка модели низкочастотными фильтрами

Использовались следующие значения масок: