Частные случаи движения
а) Прямолинейное движение.
В этом случае траекторией движения точки является прямая линия, причем ее радиус кривизны равен бесконечности (  ), следовательно:
), следовательно:
 . (1.45)
. (1.45)
Векторы скорости и ускорения в этом случае располагаются на той же прямой, что и траектория, поэтому можно говорить, что они изменяются только численно, т. е. касательное ускорение характеризует изменение скорости по модулю.
б) Равномерное криволинейное движение.
Движение называется равномерным, если точка движется с постоянной по величине скоростью. Если скорость постоянная, то, следовательно, ее производная равна нулю, т. е.:
 . (1.46)
. (1.46)
Так как в этом случае ускорение появляется только за счет изменения направления скорости, то нормальное ускорение характеризует изменение скорости по направлению.
В этом случае определим закон движения, проинтегрировав выражение (1.39)
 (1.47)
(1.47)
 . (1.48)
. (1.48)
где S0 – координата начального положения материальной точки.
Движение без ускорения (  ) возможно лишь в случае равномерного прямолинейного движения.
) возможно лишь в случае равномерного прямолинейного движения.
в) Равнопеременное криволинейное движение.
Движение называется равнопеременным, если оно происходит с постоянным касательным ускорением. Если ускорение положительно, такое движение называют равноускоренным, а если отрицательно – равнозамедленным.
В этом случае:
 , (1.49)
, (1.49)
S=  . (1.50)
. (1.50)
где V0 – скорость точки в начальный момент времени.
1.2.3. Движение материальных тел
В теоретической механике рассматриваются только абсолютно твердые тела. Движение всех материальных тел можно определенным образом классифицировать и рассматривать, как ведут себя характеристики движения применительно к каждому типу движения. Причем будем считать движение тела определенным, только в том случае, если нами определены характеристики движения всех материальных точек, составляющих рассматриваемое тело.
Поступательное движение
Поступательное движение — это такое движение, при котором любой выделенный в теле отрезок перемещается оставаясь параллельным самому себе.
Классическим примером такого движения является движение кабинок колеса обозрения (рис. 1.32.а). Этот пример наглядно показывает, что поступательное движение — совсем не обязательно прямолинейное. Число степеней свободы тела в этом случае равно трем, так как достаточно описать движение какой-нибудь одной точки тела (например, точки А на рис. 1.32.б). Траектории всех остальных точек (например, точки В на рис. 1.32.б) могут быть получены путем "параллельного" переноса.

а) б)
Рис. 1.32
Рассмотрим некоторое тело, которое движется поступательно в выбранной системе координат (рис. 1.32.б). Выберем некоторый отрезок АВ внутри тела. Положение точек А и В определяют радиус – вектора  и
и  . Пусть, закон движения точки А задан в виде
. Пусть, закон движения точки А задан в виде
 , (1.51)
, (1.51)
Тогда закон движения точки В будет иметь вид:
 . (1.52)
. (1.52)
где rАВ — вектор, проведенный от точки А к точке В.
Скорость точки А:
 . (1.53)
. (1.53)
Скорость точки В:
 . (1.54)
. (1.54)
Так как rАВ — вектор, постоянный по величине (абсолютно твердое тело) и направлению (поступательное движение), ускорения точек А и В также равны между собой:
 . (1.55)
. (1.55)
Таким образом, при поступательном движении тела законы движения всех его точек отличаются на постоянную величину, траектории при наложении совпадают, скорости всех точек равны между собой и ускорения также равны между собой.
Вращательное движение
Движение тела называют вращательным, если при его движении существуют, по крайней мере, две (а если тело плоское и движется в своей плоскости – то одна) точки тела, которые остаются неподвижными все время движения.
Линия, проходящая через эти две точки (если движение плоское, то перпендикулярно плоскости движения), называется осью вращения.
С таким движением мы сталкиваемся ежедневно, открывая и закрывая дверь в комнату. В этом случае тело обладает лишь одной степенью свободы, связанной с углом его поворота вокруг оси. При этом все точки тела движутся по окружностям, лежащим в плоскостях перпендикулярных оси вращения с центрами окружностей, лежащими на этой оси.
Существенно, что линейные скорости точек, находящихся на разном расстоянии от оси вращения, разные. В этом можно убедиться, касаясь стальной проволокой вращающегося диска точила (рис. 1.33), чем дальше от оси, тем длиннее сноп искр — тем больше скорость соответствующей точки диска.
При этом также видно, что искры летят по касательной к окружности, описываемой данной точкой диска. Ясно, что угловое перемещение всех точек твердого тела за одно и то же время будет одинаковым. Это обстоятельство позволяет ввести общую кинематическую характеристику — угловую скорость:
 , (1.56)
, (1.56)
где  - угол поворота тела за время
- угол поворота тела за время 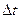 .
.


Рис.1.33 Рис.1.34
Зная  , легко определить линейную скорость любой точки твердого тела. Введем радиус-вектор rА некоторой точки А твердого тела, поместив его начало в точку О на оси вращения (рис. 1.34). Вектор r проведен в точку А от оси вращения, то есть перпендикулярно к оси. Вектор скорости VA можно связать с векторами rА и
, легко определить линейную скорость любой точки твердого тела. Введем радиус-вектор rА некоторой точки А твердого тела, поместив его начало в точку О на оси вращения (рис. 1.34). Вектор r проведен в точку А от оси вращения, то есть перпендикулярно к оси. Вектор скорости VA можно связать с векторами rА и  :
:
 , (1.57)
, (1.57)
При этом величина скорости:
 , (1.58)
, (1.58)
Очевидно, что точку О на оси вращения можно выбрать произвольно — значение r= rA sin α будет одним и тем же. Ускорение точки А:
 (1.59)
(1.59)
Здесь  угловое ускорение тела. Это вектор, направленный в ту же сторону, что и ω, если вращение ускоряется, и противоположно ему, если вращение замедляется.
угловое ускорение тела. Это вектор, направленный в ту же сторону, что и ω, если вращение ускоряется, и противоположно ему, если вращение замедляется.
Таким образом, ускорение аА является суммой двух величин:
 , (1.60)
, (1.60)
Причем все три вектора аА, аτ. и аn лежат в плоскости, перпендикулярной оси вращения (рис. 1.35).
Тангенциальное ускорение:
 , (1.61)
, (1.61)
Центростремительное ускорение:
 , (1.62)
, (1.62)
Поскольку нормальное и касательное ускорения всегда перпендикулярны друг другу, то модуль полного ускорения:

Рис. 1.35.
 . (1.63)
. (1.63)
Таким образом, определены характеристики всех точек тела при его вращательном движении.
Плоскопараллельное движение
Движение тела называется плоскопараллельным, если траектория любой точки тела располагается в определенной плоскости все время движения и плоскости движения всех точек тела совпадают или параллельны между собой.
Рассмотрим тело, которое движется плоскопараллельно (рис. 1.36), т.е. заранее можно указать такую плоскость Р, что плоскости движения всех точек тела будут параллельны этой плоскости. Возьмем некоторую точку А тела и проведем ее плоскость движения Р1, а также перпендикуляр к этой плоскости АВ.
Все точки, которые лежат на АВ, должны иметь точно такие же характеристики движения, что и точка А. В противном случае расстояние между ними невозможно было бы сохранить, поскольку они двигаются в параллельных плоскостях, и была бы нарушена гипотеза абсолютно твердого тела.

Рис. 1.36
Таким образом, задача сводится к рассмотрению движения плоского тела в своей плоскости (сечение тела плоскостью Р1 на рис. 1.36). Поэтому плоскопараллельное движение можно называть плоским.
Рассматриваем плоскую задачу о движении тела (рис. 1.37). Выберем произвольную точку этого тела А (на практике следует выбирать такую точку, характеристики движения которой заранее известны). Эту точку назовем полюс и рассмотрим как выражаются характеристики движения других точек тела через характеристики движения полюса. Проведем радиус-векторы точек А и В –  и
и  соответственно, а также вектор
соответственно, а также вектор  ,получим равенство:
,получим равенство:
 , (1.64)
, (1.64)
Продифференцировав равенство, получим:
 . (1.65)
. (1.65)
Поскольку вектор  имеет постоянный модуль (расстояние между точками А и В должно сохранятся), то
имеет постоянный модуль (расстояние между точками А и В должно сохранятся), то  можно понимать как скорость чистого вращения точки В вокруг точки А и, следовательно, плоскопараллельное движение можно разложить на составляющие: поступательное движение тела вместе с полюсом и вращательное движение тела вокруг полюса. В этом случае будем иметь, основываясь на (1.58) и (1.65)
можно понимать как скорость чистого вращения точки В вокруг точки А и, следовательно, плоскопараллельное движение можно разложить на составляющие: поступательное движение тела вместе с полюсом и вращательное движение тела вокруг полюса. В этом случае будем иметь, основываясь на (1.58) и (1.65)

Рис. 1.37.
 . (1.66)
. (1.66)
При этом законом плоскопараллельного движения тела следует считать две зависимости:  – перемещение полюса и
– перемещение полюса и  - угол поворота тела относительно некоторого заранее выбранного направления (горизонтального на рис. 1.37).
- угол поворота тела относительно некоторого заранее выбранного направления (горизонтального на рис. 1.37).
Теперь выберем в качестве полюса точку С (рис. 1.37), а угол поворота будем характеризовать некоторым углом  . Поскольку тело абсолютно твердое, то в любой момент времени должно выполняться соотношение
. Поскольку тело абсолютно твердое, то в любой момент времени должно выполняться соотношение
 , (1.67)
, (1.67)
где  .
.
Дважды последовательно продифференцировав равенство, получим:
 (1.68)
(1.68)
 (1.69)
(1.69)
Следовательно, при плоскопараллельном движении поступательная часть движения зависит от выбора полюса (  и
и  иначе движение было бы только поступательным), а вращательная часть – не зависит.
иначе движение было бы только поступательным), а вращательная часть – не зависит.
1.2.4. Теорема о проекциях скоростей двух точек тела
Теорема: проекции скоростей двух точек тела на линию, их соединяющую, равны.
Доказательство: рассмотрим движущееся тело, у которого известны в некоторый момент времени скорости точек А и В соответственно  и
и  (рис. 1.38). Если выбрать за полюс точку А, то должно выполняться равенство:
(рис. 1.38). Если выбрать за полюс точку А, то должно выполняться равенство:
 (1.70)
(1.70)

Рис. 1.38
Поскольку  - скорость чистого вращения точки В вокруг точки А, то она должна располагаться на касательной к соответствующей траектории (окружности радиусом АВ с центром в точке А), т.е. перпендикулярно линии АВ и, следовательно, ее проекция на линию АВ равна 0. Поэтому, если спроецировать вышеприведенное равенство на линию АВ, получим:
- скорость чистого вращения точки В вокруг точки А, то она должна располагаться на касательной к соответствующей траектории (окружности радиусом АВ с центром в точке А), т.е. перпендикулярно линии АВ и, следовательно, ее проекция на линию АВ равна 0. Поэтому, если спроецировать вышеприведенное равенство на линию АВ, получим:
 . (1.71)
. (1.71)
1.2.5. Мгновенный центр скоростей
Мгновенный центр скоростей – это такая точка сечения плоского тела (или жестко связанная с ним), скорость которой в данный момент времени равна нулю.
Теорема: при плоском непоступательном движении тела мгновенный центр скоростей всегда существует только один.
Доказательство: рассмотрим некоторое движущееся тело, имеющее в данный момент времени в точках А и В скорости  и
и  (рис. 1.39). Проведем перпендикуляры к векторам скоростей в этих точках – они пересекутся в некоторой точке Р. Заметим, что проекция скорости точки А на линию АР и проекция скорости точки В на ВР равны нулю.
(рис. 1.39). Проведем перпендикуляры к векторам скоростей в этих точках – они пересекутся в некоторой точке Р. Заметим, что проекция скорости точки А на линию АР и проекция скорости точки В на ВР равны нулю.

Рис. 1.39
Из теоремы о проекциях скоростей двух точек тела следует, что проекции скоростей всех точек, лежащих на линии АР также должны быть равны нулю, т. е. скорости этих точек должны быть либо перпендикулярны линии АР, либо быть равными нулю. Но, то же самое можно сказать и про точки, лежащие на ВР – их скорости либо равны нулю, либо перпендикулярны ВР. Тогда про скорость точки Р можно сказать, что она равна нулю, поскольку быть одновременно перпендикулярной двум пересекающимся прямым она не может. Точка Р и есть мгновенный центр скоростей.
Единственность мгновенного центра также следует из приведенного доказательства, так как ни для какой другой точки проекции скоростей  и
и  на линию, соединяющую их с этой точкой, будут равны нулю одновременно.
на линию, соединяющую их с этой точкой, будут равны нулю одновременно.
Следствия:
1. Для определения положения мгновенного центра скоростей необходимо знать направление скоростей двух точек тела. Мгновенный центр скоростей лежит на пересечении перпендикуляров к скоростям, проведенным из этих точек.
2. Чтобы определить угловую скорость вращения тела, необходимо знать положение мгновенного центра и величину скорости какой-либо точки тела. Угловая скорость равна отношению скорости любой точки тела к ее расстоянию до мгновенного центра скоростей. Если выбрать в качестве полюса мгновенный центр скоростей Р, то, поскольку его собственная скорость равна нулю, получим:
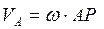 . (1.72)
. (1.72)
3. Чтобы определить скорость любой точки тела достаточно знать положение мгновенного центра скоростей и угловую скорость вращения тела. Скорость будет перпендикулярна линии, соединяющей рассматриваемую точку и мгновенный центр, а величина скорости равна произведению угловой скорости на расстояние от точки до мгновенного центра скоростей. Направление скорости следует выбирать в соответствии направлением вращения.
4. Отношение скорости любой точки тела к ее расстоянию до мгновенного центра скоростей есть величина постоянная для всех точек тела в данный момент времени. Поскольку угловая скорость не зависит от выбора полюса и одинакова для всех точек тела, то ее можно выразить через скорости различных точек:
|
(1.73)
5. Чтобы определить положение мгновенного центра в случае, когда перпендикуляры к скоростям двух точек тела слились в одну линию, необходимо дополнительно провести линию через концы векторов скоростей. Ее пересечение с перпендикуляром к скоростям и будет мгновенным центром скоростей (рис. 1.40).

Рис. 1.40.
6. Если перпендикуляры к скоростям двух точек тела оказываются параллельными прямыми (не пересекаются), а также линия АВ не перпендикулярна к VА, то это значит, что тело движется поступательно или мгновенно поступательно и говорят, что мгновенный центр скоростей лежит в бесконечности.
1.2.6. Сложное движение точки.
Движение тела называется сложным, если оно регистрируется в подвижной системе координат. При этом движение тела относительно системы координат называется относительным, а движение самой системы координат – переносным.
Рассмотрим движение точки в подвижной системе координат (рис. 1.41). За малый промежуток времени  точка переместится из положения А в положение В, но одновременно с этим ведь перемещалась и система координат. Следовательно фактически точка окажется в положении С, т. е.
точка переместится из положения А в положение В, но одновременно с этим ведь перемещалась и система координат. Следовательно фактически точка окажется в положении С, т. е. 

Рис. 1.41.
Поскольку речь идет о малых перемещениях за малые промежутки времени, с незначительной погрешностью можно считать, что  соответствует вектору абсолютной скорости
соответствует вектору абсолютной скорости  ,
,  скорости относительного движения
скорости относительного движения  ,
,  скорости переносного движения
скорости переносного движения  , т. е.
, т. е. 
Сложение скоростей.
При сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей (рис. 1.42).
|
 аб =
аб =  от +
от +  пер. (1.74)
пер. (1.74)
 Vаб =
Vаб =  . (1.75)
. (1.75)

Рис. 1.42.
Сложение ускорений (теорема Кориолиса).
При сложном движении ускорение точки равно сумме трех ускорений:
относительного, переносного, кориолисова.
 аб=
аб=  от+
от+  пер+
пер+  кор (1.76)
кор (1.76)
Относительное ускорение характеризует изменение относительной скорости только при относительном движении.
 от =
от =  . (1.77)
. (1.77)
Переносное ускорение характеризует изменение переносной скорости только при переносном движении.
 пер =
пер =  . (1.78)
. (1.78)
Кориолисово ускорение равно удвоенному произведению переносной угловой скорости на относительную скорость точки.
 кор = 2 (
кор = 2 (  ·
·  от). (1.79)
от). (1.79)
1.2.7. Пример расчета траектории движения точки.
По заданным уравнениям движения точки М установить вид ее траектории. Для момента времени t = t1, [c] определить: а) Положение точки на траектории; б) скорость точки; в) полное, касательное и нормальное ускорения; г) радиус кривизны траектории в соответствующей точке. Числовые данные варианта взять из приложения 5.
Исходные данные.
X = x (t) Y = y (t) t = 1 c.
-4t2 + 1 -3 t
Решение:
Определим положение точки М на заданной траектории в момент времени t = 1 [c]. Подставим значение t в уравнения.
x = -4 ∙ 12 + 1 = -3, y = -3 ∙ 1 = -3; М (-3;-3)
Данные уравнения являются параметрическими, то есть зависят от параметра t и характеризуют траекторию движения точки М. Чтобы получить уравнение траектории в координатной форме необходимо исключить время t.
x = - 4t2 + 1 y = - 3 t
4t2 = 1 - x t2 = (y / -3)2
t2 = (1 - x) / 4 t2 = y2/9
Так как равны левые части уравнений, то приравняем правые части:
(1 - x) / 4 = y2/9; 1 – x = (4 ∙ y2)/9; x = - (4 ∙ y2)/9 + 1.
Полученное уравнение является уравнением траектории движения точки и уравнением параболы.
Для определения скорости точки М найдем проекции скорости точки на оси координат.
v = dx / dt;
vx = (-4t2 + 1)| = - 8 t; vy = (-3 t)| = -3;
При t = 1 с проекции скорости на оси координат будут равны:
vx = - 8 см/с; vy = - 3 см/с.
Модуль полной скорости определим по формуле:
v =  ; v =
; v =  = 8,5 см/с.
= 8,5 см/с.
Для определения ускорения точки М найдем проекции ускорения точки на оси координат:
ax = (vx)| = (- 8 t)| = - 8 см/с2; ay = (vy)| = (- 3)| = 0
Модуль полного ускорения определим по формуле:
а =  ; а =
; а =  = 8 см/с2.
= 8 см/с2.
Определим нормальное и касательное ускорения.
Касательное ускорение определяется по формуле:
аt = (axvx + ayvy) / v; at = ((-8) ∙ (-8) + (-3) ∙ 0) / 8,5 = 7,5; см/с2.
Знак + (at> 0) указывает на то, что движение точки М ускоренное.
Нормальное ускорение определяется по формуле:
an =  ; an =
; an =  = 2,8 см/с2.
= 2,8 см/с2.
Определим радиус кривизны траектории движения точки М по формуле:
ρ = v2/ an; ρ = 8,52 / 2,8 = 25,8 см.
По полученным результатам стром траекторию движения точки М (рис. 1.43). Отмечаем положение точки М на ней. Изображаем ее скорости и ускорения.

Рис. 1.43.
Сведем в таблицу полученные результаты:
| Координаты | Скорости; см/с. | Ускорения; см/с2. | Радиус кривизны; см | |||||||
| x | y | vx | vy | v | ax | ay | a | at | an | ρ |
| -3 | -3 | -8 | -3 | 8,5 | -8 | 7,5 | 2,7 | 25,8 |
1.2.8. Пример расчета механизма на определение его скоростей и ускорений.
Механизм (рис. 1.44) состоит из ступенчатых колес 1, 2 и 3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны: r1= 2 см; r2 = 6 см; r3 =12 см; R1 =4с м; R2 = 8 см; R3 = 16 см. На ободьях колес расположены точки А, В и С. Числовые данные варианта взять из приложений 6 и 7. Схему варианта из приложения 8. Определить в момент времени t1 = 2с указанные в таблице скорости и ускорения соответствующих точек или тел.
Схема нагружения и исходные данные.

Рис. 1.44
Закон вращения колеса: φ1 = 2t2-9; Найти: v4, ω2, ε2, ас, а5.
Решение:
Составим расчетную схему:

Рис. 1.45
Определим значение угловой скорости второго колеса, ω2: для этого определим закон изменения угловой скорости первого колеса:
ω1 = (φ1)|;
ω1 = (2t2-9)| = 4t.
Так как колесо 1 связано с колесом 3 ременной передачей, а ремень во всех точках имеет постоянную линейную скорость, то можно записать равенство:
v1 = v3;
Так как ремень соединяет колеса 1 и 3 по радиусам r1 и r2, то линейные скорости будут равны:
v1 = ω1 ∙ r3; v3 = ω3 ∙ r3,
Так как равны левые части, то приравняем правые части равенств:
ω1 ∙ r1 = ω3 ∙ r3;
Выразим ω3:
ω3 = ω1 ∙ r1 / r3 = 4 t ∙ 2 / 12 = 2/3 t.
Второе и третье колеса связаны непосредственно по радиусам R2 и R3, аналогично определим закон изменения угловой скорости второго колеса:
v2 = v3;
v2 = ω2 ∙ R2; v3 = ω3 ∙ R3;
ω 2 = ω3 ∙ R3 / R2; ω 2 = (2/3 t ∙ 16) / 8 = 4/3 t,
При t = 2 с: ω 2 = 8 / 3 = 2,7; с-1.
Определим линейную скорость рейки, v4:
Так как рейка 4 находится в зацеплении с первым колесом по радиусу R1, то в месте их зацепления линейные скорости колеса и рейки будет равны:
v4 = v1; v1 = ω1 ∙ R1 = 4 t ∙ 4 = 16 t,
При t = 2 с: v4 = 16 ∙ 2 = 32; см/с.
Определим значение углового ускорения второго колеса, ε2:
ε2 = (ω 2)| = (4/3 t)| = 4/3 = 1,3; с-2.
Определим линейное ускорение заданной точки С, ас:
ас =  ,
,
где a ct - линейное касательное ускорение точки С, см/с2;
a cn - линейное нормальное ускорение точки С, см/с2;
Так как точка С находится на втором колесе на радиусе R2, то:
act = ε2 ∙ R2 = 4/3 ∙ 8 = 10,7 см/с2;
acn = ω22 ∙ R2 = (4/3 t)2 ∙ 8
При t = 2 с: acn = (4/3 ∙ 2)2 ∙ 8 = 56,9 см/с2,
ас =  = 57,9 см/с2.
= 57,9 см/с2.
Определим линейное ускорение груза 5, а5:
а5 = (v5)|;
Так как нить, удерживающая груз 5 намотана на второе колесо на радиусе r2, то в точке закрепления нити линейные скорости второго колеса и груза 5 равны:
v5 = v2,
v5 = ω2 ∙ r2 = 4/3 t ∙ 6 = 8 t,
а5 = (8 t)| = 8 см/с2.
Ответ: v4 = 32, см/с; ω 2 = 2,7, с-1; ε2 = 1,3, с-2; ас = 57,9, см/с2; а5 = 8, см/с2.
Динамика
Динамика изучает движение материальных тел как результат их взаимодействия с другими телами.
Так как мерой взаимодействия является сила, то поведение сил и изменение характеристик движения во времени должны быть взаимосвязаны.
Все задачи динамики можно условно разделить на две категории:
- зная характеристики движения, определить силы, вызвавшие такое движение (прямая задача);
- зная силы, определить характеристики движения (обратная задача).
При рассмотрении статики силы считались постоянными величинами, в динамике будем учитывать, что сила – величина переменная.
1.3.1. Аксиомы динамики
Аксиома №1: сила – это векторная величина.
Следовательно, с силами можно совершать те же операции, что и с векторами, т.е. складывать, вычитать, проецировать, умножать на скаляр или другой вектор и т.д.
Аксиома №2: любое материальное тело можно представить как совокупность конечного числа материальных точек.
Аксиома №3: если силы, действующие на материальную точку, уравновешены или отсутствуют, то эта точка сохраняет состояние покоя или движется равномерно и прямолинейно (по инерции).
Движение равномерное и прямолинейное называется инерционным движением.
Система координат, в которой выполняется первая аксиома, называется инерционной системой отсчета. Не все системы координат являются инерционными, поэтому чтобы пользоваться теоремами и законами динамики, необходимо выбрать систему координат. На практике следует учитывать, что инерционной можно считать только систему координат с центром в центре масс Солнца и осями, направленными на удаленные внегалактические объекты. Систему координат, располагающуюся на поверхности земли, можно считать инерционной условно. При этом погрешность расчетов подавляющего большинства задач о движении тел вблизи поверхности Земли будет достаточно мала.
Аксиома №4: если на материальную точку действует сила, то эта точка будет двигаться с ускорением, прямо пропорциональным этой силе. Коэффициент пропорциональности между силой  и ускорением
и ускорением  называется массой материальной точки m.
называется массой материальной точки m.
 . (1.80)
. (1.80)
Поскольку в теоретической механике рассматриваются тела, движущиеся со скоростями только гораздо меньше скорости света, то массу можно считать постоянной величиной.
Возьмем две материальные точки с различными массами, например m1>m2, и подействуем на каждую из них одной и той же силой  . На основании четвертой аксиомы получим:
. На основании четвертой аксиомы получим:
 (1.81)
(1.81)
Видим, что чем больше масса точки, тем медленнее она будет двигаться под действием одной и той же силы при прочих равных условиях.
Инертность – это способность тел сопротивляться попыткам изменить их состояние.
Масса является мерой инертности поступательного движения тел. Чем больше масса, тем труднее привести тело в движение и труднее, затем остановить его.
Аксиома №5: две материальные точки действуют друг на друга с силами равными по величине, лежащими на одной прямой и направленными в разные стороны (действие равно противодействию).
1.3.2. Уравнения движения точки в декартовой системе координат
Рассмотрим движение материальной точки. Пусть на нее действуют силы  . Так как речь идет о материальной точке, то эти силы обязательно будут сходящимися, и их можно заменить равнодействующей:
. Так как речь идет о материальной точке, то эти силы обязательно будут сходящимися, и их можно заменить равнодействующей:
 (1.82)
(1.82)
где i = от 1 до n.
На основании четвертой аксиомы имеем:
 (1.83)
(1.83)
Как известно из кинематики,  , тогда:
, тогда:
 (1.84)
(1.84)
Если перейти к проекциям, то получим систему дифференциальных уравнений второго порядка, описывающих поведение материальной точки вдоль каждой из осей координат:
 . (1.85)
. (1.85)
1.3.3. Одномерное движение
Движение точки будет одномерным, если для его описания достаточно одной оси координат, траектория будет прямой линией.
Выбираем систему координат так, чтобы ось Х совпала с траекторией движения. Тогда движение точки может быть описано уравнением:
 , (1.86)
, (1.86)
где Fx – сумма проекций всех сил на ось Х.
Масса m - величина постоянная, а сила Fx – величина переменная. Рассмотрим только те силы, которые могут зависеть от времени, скорости и координат положения точки приложения силы  .
.
При решении и прямой, и обратной задач динамики используется уравнение (1.86). Решая прямую задачу, приходится выполнять операцию дифференцирования, а при решении обратной задачи – операцию интегрирования. Поскольку реальные законы движения и скорости материальных точек являются гладкими непрерывными функциями, то дифференцирование всегда осуществимо и, следовательно, прямая задача всегда может быть решена аналитически. А вот проинтегрировать можно далеко не всякую даже гладкую функцию, поэтому обратную задачу не всегда можно решить аналитически, ее решение сильно зависит от особенностей действующих сил.
Кроме того, операция интегрирования выполняется с точностью до константы, поэтому уравнение (1.86) необходимо дополнять начальными условиями. В любой задаче механики при решении обратной задачи начальные условия считаются заданными, если начальные значения отсутствуют, то можно принять любые значения.
1.3.4. Уравнения материальной точки в естественной системе координат
Если уравнение (1.84) разложить по осям естественной системы координат, получим:
 , (1.87)
, (1.87)
Учитывая особенности разложения вектора ускорений в естественной системе координат получим:
 , (1.88)
, (1.88)
где S – закон движения в естественной системе координат.
1.3.5. Колебательное движение материальной точки
При движении материальной точки может действовать упругая сила, стремящаяся вернуть точку к некоторому положению. Эта упругая сила называется восстанавливающей. В большинстве задач рассматривается восстанавливающая сила F, изменяющаяся по линейному закону (закону Гука) (рис. 1.46). При растяжении пружины эта сила прямо пропорциональна удлинению:
F = -сΔ, (1.89)
где Δ — смещение конца пружины из ненапряженного состояния,
с — коэффициент упругости (коэффициент жесткости), численно равный силе, которую надо приложить к пружине для того, чтобы изменить ее длину на единицу, кг/см.

Рис. 1.46
Вообще линейной восстанавливающей называется сила, стремящаяся вернуть точку в положение равновесия и пропорциональная отклонению этой точки от положения равновесия.
Свободные колебания материальной точки.
Свободными называются колебания материальной точки, которые происходят под действием восстанавливающей силы. При движении материальной точки М массой m по горизонтальной оси х (рис. 1.47) под действием восстанавливающей силы F, равной по модулю  (О-положение равновесия точки М), имеет место дифференциальное уравнение движения:
(О-положение равновесия точки М), имеет место дифференциальное уравнение движения:
 , (1.90)
, (1.90)
где 

Рис. 1.47
При начальных условиях движения материальной точки, записанных в виде: t = 0, x = x0,  закон ее свободных колебаний имеет вид:
закон ее свободных колебаний имеет вид:
 (1.91)
(1.91)
т. е. материальная точка совершает гармоническое колебательное движение; а - амплитуда колебаний — наибольшее отклонение колеблющейся точки от положения равновесия:
 (1.92)
(1.92)
 - фаза колебаний; α – начальная фаза колебаний.
- фаза колебаний; α – начальная фаза колебаний.
Периодом колебаний Т материальной точки называется наименьший промежуток времени, по истечении которого точка имеет ту же координату и ту же проекцию скорости:
 . (1.93)
. (1.93)
Вынужденные колебания материальной точки. Возмущающая сила.
В теории колебаний возмущающей называется сила, приложенная к материальной точке и заданная как функция времени. Эта сила большей частью является непрерывной функцией времени (рис. 1.48).

Рис. 1.48
В механизмах возмущающаяся сила возникает в результате неточной балансировки вращающихся частей машин (турбинных дисков, роторов электромоторов, маховиков), либо при наличии периодически изменяющейся силы давления воды, газа или пара в цилиндрах двигателей и т. д.
Простейшей является возмущающая сила S, изменяющаяся по гармоническому закону:
 (1.94)
(1.94)
где Н — наибольшая величина возмущающей силы (амплитуда силы), кг,
р — круговая частота изменения возмущающей силы, сек-1,
δ — начальная фаза.
Вынужденные колебания материальной точки вызываются действием системы сил, в составе которой имеются восстанавливающая сила F и возмущающая сила S. На рис. 1.49 ось х направлена вдоль линий действия сил F и S. Начало отсчета выбрано в положении статического равновесия материальной точки.  Сила S условно направлена вниз, однако, как следует из закона ее изменения, направление является переменным.
Сила S условно направлена вниз, однако, как следует из закона ее изменения, направление является переменным.
Дифференциальное уравнение вынужденных к
Дата добавления: 2022-05-27; просмотров: 127;

 .
.










