Характеристики импульсных систем, описываемых уравнениями в пространстве состояний

Если в первом уравнении (1.80), которое является неоднородным разностным уравнением считать матрицу 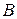нулевой, то получим однородное разностное уравнение

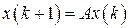, (1.91)

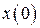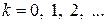в котором, полагая заданным начальное состояние вектора при , получим 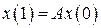, , 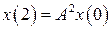и т.д. Таким образом, общее решение уравнения (1.91) можно записать в виде

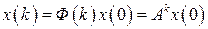. (1.92)

Матрица 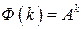носит название переходной матрицы состояния линейной импульсной системы. Вычисление 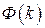по известной матрице 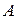всегда возможно. Наиболее просто найти 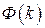, если матрица 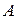диагональная. Если 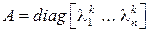, то .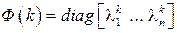

Если найдена 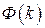, то в импульсной системе, описываемой уравнениями (1.80), можно вычислить выход 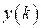при заданном входе 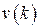по выражению

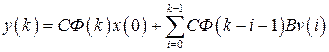. (1.93)

В (1.93) первое слагаемое − свободная составляющая, а второе − вынужденная.

Применим к уравнениям (1.80) 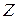-преобразование, полагая, что начальные значения вектора состояния 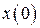нулевые. Получим 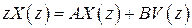, , 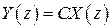где 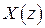, , 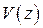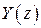− изображения соответствующих векторов , , .

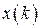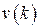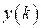Из полученного уравнения найдем

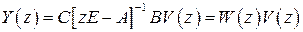, (1.94)

где 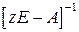− обратная матрица к матрице 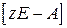, 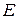− единичная 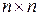матрица.

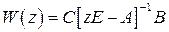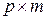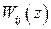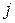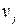Матрица размерности носит название передаточной матрицы (матрицы передаточных функций) импульсной системы. Ее элементы являются обычными скалярными функциями, связывающими вход с 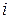выходом 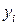. Если 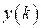, 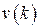− скалярные величины, то 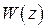− обычная скалярная передаточная функция.

Матрицу 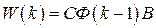будем называть весовой матрицей. Очевидна связь

, .

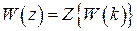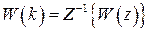Отметим один из способов определения переходной матрицы состояния 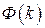с помощью 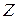-преобразования

.

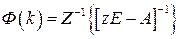Введем еще одну из важнейших характеристик импульсной системы, заданной уравнениями состояния (1.80), – характеристическое уравнение импульсной системы

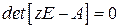, (1.95)

где 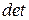означает определитель матрицы 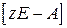. Если матрица 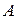размерности 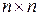, то (1.95) − это алгебраическое уравнение 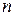-ой степени.

Линейная импульсная система, описываемая уравнениями состояния (1.80), будет устойчива, если все корни 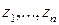уравнения (1.95) по модулю меньше единицы, т.е. 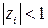, 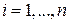. Для выяснения этого факта можно, например, использовать алгебраический критерий устойчивости импульсных систем, изложенный в подразделе 1.7.

Для импульсных систем, описываемых уравнениями (1.80), можно ввести и другие понятия, аналогичные понятиям для непрерывных систем [1], такие как наблюдаемость и управляемость. Управляемость и наблюдаемость зависят от вида матриц 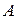, , 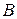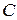в (1.80). Определения и методы оценки управляемости и наблюдаемости идентичны [1] и здесь не приводятся.

Пример 1.13. Найдем передаточную функцию разомкнутой импульсной системы из примера 1.12, используя полученные уравнения состояния (1.90). В соответствии с (1.94) 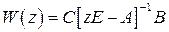. Найдем матрицу 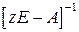. Очевидно,

.

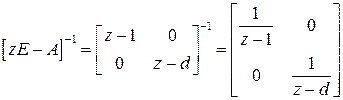С учетом матриц 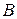и 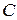из (1.90) имеем

,

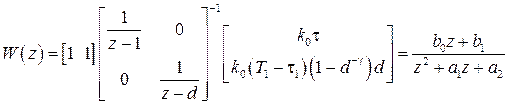где , , , .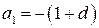

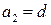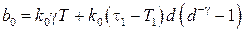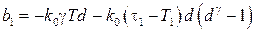Этот результат совпадает с результатом, полученным в примере 1.2.