Первый замечательный предел
Определение 1. Функция 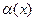 называется бесконечно малой в окрестности точки
называется бесконечно малой в окрестности точки 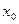 , если
, если 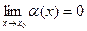 .
.
Например, 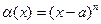 – бесконечно малая функция в окрестности точки
– бесконечно малая функция в окрестности точки 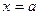 , так как
, так как 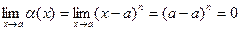 .
.
Теорема 1. Для того чтобы 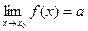 , необходимо и достаточно, чтобы имело место представление
, необходимо и достаточно, чтобы имело место представление 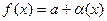 , где
, где 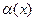 – бесконечно малая в окрестности точки
– бесконечно малая в окрестности точки 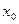 функция.
функция.
Доказательство. Необходимость. Пусть 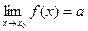 . Положим
. Положим 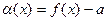 .
.
Тогда 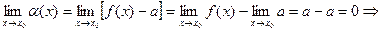
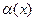 – бесконечно малая в окрестности точки
– бесконечно малая в окрестности точки 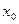 функция и
функция и 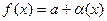 .
.
Достаточность. Пусть 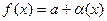 , где
, где 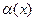 – бесконечно малая в окрестности точки
– бесконечно малая в окрестности точки 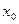 функция. Тогда
функция. Тогда 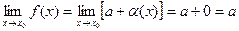 . Теорема доказана.
. Теорема доказана.
Остановимся на сравнении бесконечно малых функций.
Определение 2. Говорят, что функции 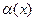 и
и 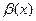 являются эквивалентными бесконечно малыми в окрестности точки
являются эквивалентными бесконечно малыми в окрестности точки 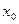 функциями, если
функциями, если 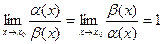 .
.
Пишут: 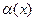 ~
~ 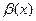 при
при 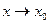 .
.
Определение 3. Говорят, что функции 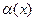 и
и 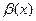 являются в окрестности точки
являются в окрестности точки 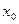 бесконечно малыми функциями одного порядка, если
бесконечно малыми функциями одного порядка, если 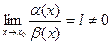 . Если же
. Если же 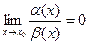 , то говорят, что
, то говорят, что 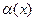 является в окрестности точки
является в окрестности точки 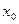 бесконечно малой более высокого порядка, чем
бесконечно малой более высокого порядка, чем 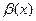 .
.
Покажем, что 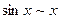 при
при 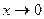 .
.
Теорема 2 (первый замечательный предел). Справедливо равенство 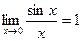 .
.
|
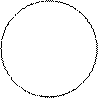
 Доказательство. Построим единичный круг и центральный угол
Доказательство. Построим единичный круг и центральный угол 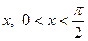 .
.
| |||
 | |||
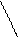
|
|
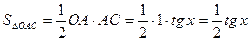 . (16.4)
. (16.4)
Из (16.1)–(16.4) получаем
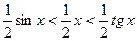 .
.
Разделив последнее неравенство на 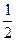 , получим
, получим
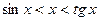 . (16.5)
. (16.5)
Разделив 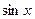 на каждую из частей этого неравенства, имеем
на каждую из частей этого неравенства, имеем
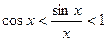 . (16.6)
. (16.6)
Поскольку 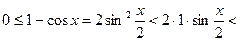 (см. (16.5))
(см. (16.5)) 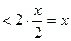 и
и 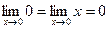 , по
, по
Теореме о промежуточной переменной 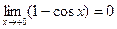 , то есть
, то есть 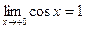 . А так как
. А так как
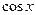 – функция четная, то
– функция четная, то 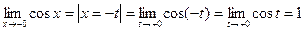 . Поэтому
. Поэтому
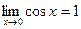 . (16.7)
. (16.7)
Учитывая, что неравенство (16.6) сохраняется и для 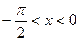 в силу четности всех входящих в него функций, из (16.7) и теоремы о промежуточной переменной получаем
в силу четности всех входящих в него функций, из (16.7) и теоремы о промежуточной переменной получаем 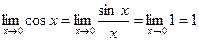 . Теорема доказана.
. Теорема доказана.
Установим теперь следствия первого замечательного предела. Покажем, что при 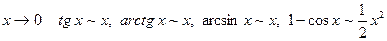 . Имеем
. Имеем
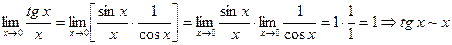 при
при 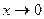 ;
;
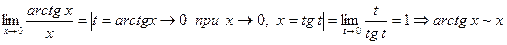 при
при 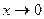 ;
;
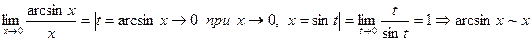 при
при 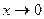 ;
;
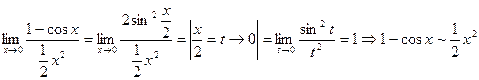 при
при 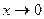 .
.
При раскрытии неопределенностей типа 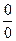 полезна
полезна
Теорема 3. Если 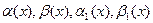 – бесконечно малые функции в окрестности точки
– бесконечно малые функции в окрестности точки 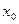 и
и 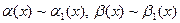 , то
, то
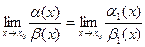 .
.
Доказательство. Имеем
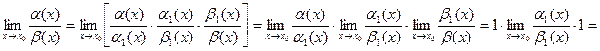
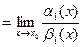 . Теорема доказана.
. Теорема доказана.
Например, 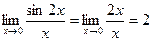 .
.
Замечание. В тех случаях, когда в числителе или знаменателе записана сумма, при раскрытии неопределенностей нельзя заменять отдельные слагаемые эквивалентными функциями, так как такая замена может привести к неверному результату. Например, в пределе  нельзя заменить
нельзя заменить 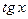 на
на 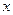 и
и 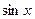 на х, так как получается выражение
на х, так как получается выражение 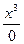 , не имеющее смысла. Правильно вычислять предел так:
, не имеющее смысла. Правильно вычислять предел так:
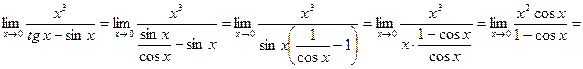
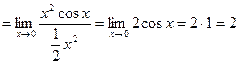 .
.
Рассмотрим теперь бесконечно большие функции.
Определение 4. Если для любой последовательности значений аргумента 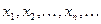 , сходящейся к
, сходящейся к 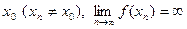 , то говорят, что функция
, то говорят, что функция 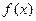 имеет в точке
имеет в точке 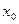 бесконечный предел, а функцию
бесконечный предел, а функцию 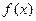 называют бесконечно большой при
называют бесконечно большой при 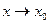 . Пишут:
. Пишут: 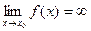 .
.
Можно дать равносильное
Определение 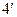 . Говорят, что функция
. Говорят, что функция 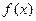 имеет в точке
имеет в точке 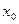 бесконечный предел, если для любого числа
бесконечный предел, если для любого числа 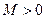 найдется такое число
найдется такое число 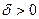 , что для всех значений
, что для всех значений 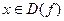
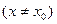 , удовлетворяющих неравенству
, удовлетворяющих неравенству 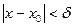 , выполняется неравенство
, выполняется неравенство 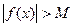 . В этом случае
. В этом случае 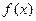 называется бесконечно большой функцией в точке
называется бесконечно большой функцией в точке 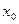 .
.
Аналогично определяются соотношения 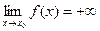 ,
, 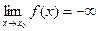 .
.
Сравнивают бесконечно большие функции так же, как и бесконечно малые функции.
Определение 5. Если 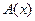 и
и 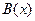 – бесконечно большие функции при
– бесконечно большие функции при 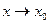 и
и 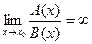 , то говорят, что
, то говорят, что 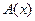 – бесконечно большая более высокого порядка, чем
– бесконечно большая более высокого порядка, чем 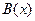 . Говорят, что функции
. Говорят, что функции 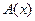 и
и 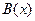 имеют одинаковый порядок роста, если
имеют одинаковый порядок роста, если 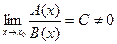 .
.
Например, для функций 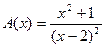 и
и 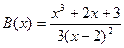 , бесконечно больших при
, бесконечно больших при 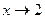 , имеем
, имеем 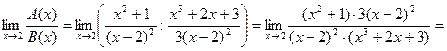
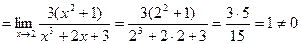 , поэтому функции
, поэтому функции 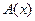 и
и 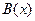 имеют одинаковый порядок роста.
имеют одинаковый порядок роста.
Дата добавления: 2016-06-09; просмотров: 1266;

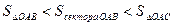 . (16.1)
Имеем
. (16.1)
Имеем
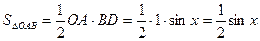 , (16.2)
, (16.2)
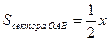 , (16.3)
, (16.3)









