Универсальная машина Тьюринга

Я еще не затрагивал понятия универ­сальной машины Тьюринга. Лежащий в ее основе принцип понять нетрудно, хотя де­тали могут быть сложны. Основная идея состоит в том, чтобы закодировать коман­ды для произвольной машины Тьюринга Т в виде последовательности нулей и единиц, которую можно записать на ленте. Эта за­пись используется как начальная часть вход­ных данных для некоторой особой маши­ны Тьюринга U, называемой универсаль­ной, которая затем обрабатывает остальную часть ленты в точности так, как это сде­лала бы машина Т. Универсальная маши­на Тьюринга — это универсальный ими­татор. Начальная часть ленты дает уни­версальной машине U всю информацию, необходимую для точной имитации любой машины Т!

Чтобы показать, как это может быть реализовано, нам потребуется какая-нибудь система нумерации машин Тьюринга. Рас­смотрим список инструкций, определяющих произвольную машину Тьюринга, напри­мер, одну из описанных выше. Мы должны в соответствии с некоторыми четкими пра­вилами представить эти инструкции в виде последовательностей нулей и единиц. Это можно сделать, например, с помощью про­цедуры «сокращения», которую мы исполь­зовали ранее. Тогда, если мы закодируем символы R, L, STOP, «стрелка» (->) и «за­пятая», скажем, числами 2, 3, 4, 5 и 6 со­ответственно, то мы сможем записать их в виде «сокращений» 110, 1110, 11110, 111110 и 1111110.Цифры 0 и 1, коди­руемые, соответственно, как 0 и 10, могут быть использованы для записи строк этих символов, входящих в таблицу действий ма­шины Тьюринга. Нам не нужны различ­ные обозначения для «жирных» цифр 0 и 1 и для остальных цифр в таблице, посколь­ку расположение «жирных» цифр в конце двоичного кода является достаточным отли­чительным признаком. При этом 1101, на­пример, будет читаться как двоичное число 1101, представляемое на ленте последова­тельностью 1010010. Вчастности, 00 будет читаться как 00, что без всякой двусмы­сленности можно закодировать как 0 или вовсе опустить. Можно существенно сэко­номить, если не кодировать «стрелки» и не­посредственно предшествующие им симво­лы, а воспользоваться цифровым упорядо­чением команд, позволяющим определить, какими должны быть эти символы. Правда, для этого надо убедиться в отсутствии «ды­рок» в получившемся порядке и добавить, где требуется, «немые» команды. (Напри­мер, машина Тьюринга XN + 1 не имеет команды, соответствующей коду 1100, по­скольку такая комбинация в ходе ее работы никогда не встречается. Следовательно, мы должны ввести в список команд немую ко­манду, скажем 1100 -> OOR, которая не вы­зовет каких бы то ни было изменений в ра­боте машины. Сходным образом мы должны добавить немую команду 101 —> OOR в спи­сок команд машины XN x 2.) Без таких «не­мых» команд кодирование последующих ко­манд было бы нарушено. Как можно видеть, на самом деле мы не нуждаемся и в запятой в конце каждой команды, поскольку симво­лов L и R вполне достаточно для отделения команд друг от друга. Поэтому мы просто будем использовать такую систему кодиро­вания:

В качестве примера выпишем команды для машины Тьюринга XN + 1 (с допол­нительной немой командой 1100 -+ OOR). Опуская стрелки, цифры, непосредственно предшествующие им, и запятые, получим

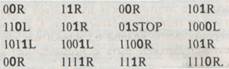
Мы можем улучшить полученный результат, если опустим все 00 и заменим каждые 01 просто единицей в соответствии с тем, что говорилось ранее. Тогда мы получим строку символов

которая на ленте записывается как последо­вательность

Есть еще два способа немного сэконо­мить. Во-первых, всегда можно удалить код 110 в начале записи (вместе с бесконечным участком пустой ленты, предшествующим этому коду). Он обозначает последователь­ность OOR, соответствующую начальной ко­манде 00 —> OOR, которую я до сих пор неявно считал общей для всех машин Тью­ринга, поскольку она необходима для того, чтобы устройство, начав работу в произволь­ной точке слева от начала записи на ленте, могло перемещаться вправо до тех пор, по­ка не встретит первую непустую клетку. Во-вторых, точно так же всегда можно удалить код 110 (и неявную бесконечную после­довательность нулей, которая, по предпо­ложению, следует за ним) в конце записи, поскольку этой кодовой последовательно­стью должно заканчиваться описание любой машины Тьюринга (во всех случаях спи­сок команд заканчивается командой R, L или STOP). Получающееся двоичное число — это номер машины Тьюринга, который для XN + 1 будет выглядеть так:

В обычной десятичной записи этот номер равен:

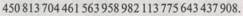
Иногда машину с номером п мы, не вполне точно, будем называть n-й машиной Тьюринга и обозначать ее Т_п В этом случае XN + 1 становится

машиной Тьюринга!

Кажется поразительным факт, что нам надо пробежать так долго вдоль «списка» ма­шин Тьюринга, чтобы найти машину, вы­полняющую такую тривиальную операцию, как прибавление единицы к натуральному числу (в расширенном двоичном предста­влении). (Я не думаю, что моя система коди­рования была в целом настолько неэффек­тивна, хотя в ней и есть еще возможности для незначительных улучшений.) В действи­тельности, есть машины Тьюринга и с мень­шими номерами, которые представляют ин­терес, например UN + 1 с двоичным но­мером

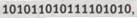
который в десятичной записи превращает­ся всего лишь в 177 642. Значит, особенно тривиальная машина UN + 1, которая про­сто дописывает 1 единицу в конце после­довательности единиц, является 177 642-й машиной Тьюринга. Интересно, что «умно­жение на два» в списке машин Тьюринга попадает где-то между этими двумя маши­нами, причем и в унарном, и в расширен­ном двоичном представлении: номер XN x 2 равен 10 389 728 107, а номер UN x 2 -1492 923 420 919 872 026 917 547 669.

Наверное, принимая во внимание вели­чины этих номеров, уже не вызовет удивле­ния тот факт, что абсолютное большинство натуральных чисел не соответствует ни од­ной рабочей машине Тьюринга. Приведем перечень первых тринадцати машин Тью­ринга в соответствии с принятой нумера­цией:

Из этих машин T₀ просто перемеща­ется вправо, стирая все, что ей попада­ется на пути, никогда не останавливаясь и не меняя направления движения. Маши­на Т₁ выполняет в сущности ту же опе­рацию, но более громоздким путем, от­ступая на шаг назад каждый раз, когда она стирает очередную единицу на ленте. Так же как и T₀, машина T₂двигается впра­во, никогда не останавливаясь, но относит­ся к ленте более «почтительно», попросту оставляя всю информацию нетронутой. Эти машины не могут использоваться в каче­стве машин Тьюринга, поскольку никогда не останавливаются. Т₃, -- первая в этом списке «правильная» машина: она скром­но прекращает действие после того, как изменяет первую (самую левую) единицу на нуль. t₄ сталкивается с серьезной пробле­мой. Найдя первую единицу на ленте, она переходит во внутреннее состояние, которое нигде не описано, и, следовательно, маши­на не имеет никаких команд для следующего шага. С той же проблемой сталкиваются T₈, Т₉ и Т_10. С T₇ возникают трудности еще более фундаментального характера. Строка нулей и единиц, которой она представля­ется, включает последовательность из пяти единиц: 110111110.Интерпретации этой последовательности не существует, поэто­му Т₇ намертво застревает сразу же, как только доходит до первой единицы. (Я бу­ду называть Т₇, равно как и любую другую машину Т_n, двоичное расширенное пред­ставлений которой содержит более четырех единиц, некорректно определенной.) Маши­ны Т₅, T₆, и Т₁₂ испытывают те же трудно­сти, что и Т₀, Т₁, t₂ они просто никогда не останавливаются. Все эти машины — T₀, T₁ Т₂, Т₅, Т₆, Т₇, Т₈, Т₉, Т₁₀ и Т₁₂ -совершенно бесполезные устройства! Толь­ко Т₃ и Т₁₁ являются функциональными машинами Тьюринга, да и то не слишком интересными. Причем Т₁₁ даже скромнее, чем Т₃: натолкнувшись на первую же еди­ницу, она останавливается и вообще ничего не меняет!

Надо заметить, что наш перечень содер­жит избыточную информацию. Машина Т₁₂ идентична T₆, а по действиям обе они ана­логичны Т₀, поскольку ни T₆, ни T₁₂ нико­гда не переходят во внутреннее состояние 1. Но нам нет нужды волноваться из-за этой избыточности, равно как из-за изобилия не­работоспособных (фиктивных) машин Тью­ринга в нашем списке. На самом деле, мы могли бы изменить систему кодирования та­ким образом, чтобы избавиться рт большого числа бесполезных устройств и значитель­но уменьшить избыточность списка машин. Но все это можно сделать только ценой усложнения нашей примитивной универ­сальной машины Тьюринга, которая долж­на расшифровывать вводимую в нее запись и имитировать машину Т_п, чей номер она считала. Это было бы оправдано, если бы было можно избавиться от всех бесполезных (и повторяющихся) машин. Но это, как мы увидим чуть позднее, невозможно! Поэтому мы оставим нашу систему кодирования без изменений.

Будет удобно интерпретировать ленту с последовательностью меток на ней, на­пример

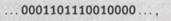
как двоичное представление некоторого чи­сла. Вспомним, что нули простираются бес­конечно в обе стороны, а вот количество единиц конечно. Кроме того, я буду пола­гать, что их число отлично от нуля (т. е. что в этой последовательности существует хотя бы одна единица). Мы можем тогда считывать конечную строку символов меж­ду первой и последней единицами (включи­тельно) , которая в предыдущем случае имеет вид

как двоичное представление натурального числа (в десятичной форме это 441). Однако такая процедура даст нам только нечетные числа (их двоичное представление оканчи­вается на 1), тогда как нам нужна воз­можность представления всех натуральных чисел. Поэтому мы воспользуемся следую­щим несложным приемом — будем удалять последнюю единицу (которая принимается просто за маркер, обозначающий конец вы­ражения) и считывать оставшуюся часть как двоичное число. Тогда в последнем при­мере получим двоичное число

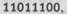
которое соответствует десятичному числу 220. Эта процедура имеет то преимущество, что нуль также представляется непустой лен­той, а именно:

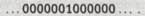
Рассмотрим, как действует машина Тьюринга Т_п на некоторую (конечную) строку нулей и единиц на ленте, которая подается в устройство справа. Удобно рас­сматривать эту строку как двоичное пред­ставление некоторого числа, например т, в соответствии с приведенной выше схе­мой. Предположим, что после определенно­го числа шагов машина Т_п в конце концов останавливается (т. е. доходит до команды STOP). Строка двоичных цифр, которые ма­шина выписала к этому моменту на левой части ленты, и будет искомым результатом вычислений. Считывая эту последователь­ность в соответствии с той же схемой так же как двоичное представление некоторого чи­сла, получим новое число, скажем, р. Тогда мы можем записать соотношение, выражаю­щее тот факт, что результатом действия n-й машины Тьюринга Т_п на число m является число р, следующим образом:

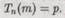
Взглянем на это соотношение с не­сколько иной точки зрения. Мы будем счи­тать, что это выражение описывает неко­торую специфическую операцию, которая применяется к паре чисел пит для того, чтобы получить р. (Это означает: для задан­ных двух чисел тип мы можем найти зна­чение р, если введем m в n-ю машину Тью­ринга.) Эта специфическая операция явля­ется полностью алгоритмической. Поэтому она может быть выполнена одной конкрет­ной машиной Тьюринга U; иными слова­ми, U, совершая действие над парой (п, т), дает в результате р. Поскольку машина U должна производить операцию над обоими числами пит, чтобы получить ответ, вы­ражаемый одним числом р, то нам нужно придумать способ для записи пары (n, m) на одной ленте. С этой целью предположим, что п записывается в стандартной двоич­ной форме и заканчивается последователь­ностью 111110.(Вспомним, что двоичный номер всякой корректно определенной ма­шины Тьюринга, — это последовательность символов, состоящая только из сочетаний вида 0, 10, 110, 1110 и 11110,поэтому он нигде не содержит более четырех единиц подряд. Таким образом, если Т„ -- кор­ректно определенная машина, то появление последовательности 111110действительно будет означать конец записи номера те.) Все, что следует за ней, должно быть просто за­писью числа то на ленте в соответствии с приведенными выше правилами (т. е. дво­ичное число m и строка 1000... непо­средственно за ним). Таким образом, с этой второй частью ленты машина Т_n и должна производить предполагаемые действия.

Если в качестве примера мы возьмем n = 11 и m = 6, то на ленте, вводимой в машину U, мы будем иметь последова­тельность

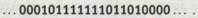
Она образована из следующих составляю­щих:

То, что машина Тьюринга U должна была бы делать на каждом очередном ша­гу процедуры, выполняемой Т_n над m —

это исследовать структуру последователь­ности цифр в выражении п с тем, чтобы можно было произвести соответствующие изменения цифр числа m (т. е. «ленты» ма­шины Т_n). В принципе, реализация такой I машины не вызывает существенных затруд- I нений (хотя и довольно громоздка на прак­тике). Список ее собственных команд дол­жен был бы просто содержать правила для чтения подходящей команды из «списка», закодированного в числе п, на каждом эта­пе выполнения действий над цифрами, счи-1 тайными с «ленты», как они фигурируют в числе т. Можно предположить, что при этом совершалось бы значительное количе­ство прыжков взад-вперед по ленте между цифрами, составляющими те и т, и выполнение процедуры было бы чрезвычайно медленным. Тем не менее, список команд подобной машины, несомненно, можно составить, и такая машина называется нами универсальной машиной Тьюринга. Обозна­чая ее действие на пару чисел (n, т) через U(n, т), мы получаем:

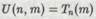
при любых (п, т), для которых T_n — кор­ректно определенная машина Тьюринга. Машина U, в которую первым вводится чи­сло те, в точности имитирует n-ю машину Тьюринга!

Поскольку U — машина Тьюринга, то она сама будет иметь номер. То есть, для некоторого числа и имеем

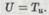
Сколь велико n? В сущности, мы можем по­ложить, что и в точности равно следующему числу:

и=24485533533931757719839503961571123 7952360672556559631108144796606505059404 2410903104836136323593656444434583822268 8327876762655614469281411771501784255170 7554085657689753346356942478488597046934 7257399885822838277952946834605210611698 3594593879188554632644092552550582055598 9451890716537414896033096753020431553625 0349845298323206515830476641421307088193 2971723415105698026273468642992183817215 7333482823073453713421475059740345184372 3595930906400243210773421788514927607975 763441512307958639635449226915947965461

4711345700145048167337562172573464522731 0544829807849651269887889645697609066342 0447798902191443793283001949357096392170 3904833270882596201301773727202718625919 9144282754374223513556751340842222998893 7441053430547104436869587640517812801943 7530813870639942772823156425289237514565 4438990527807932411448261423572861931183 3261065612275553181020751108533763380603 1082361675045635852164214869542347187426 4375444287900624858270912404220765387542 6445413345174856629157429990950262300973 3738137724162172747723610206786854002893 5660856968226201419824862169890260913094 0298570600174300670086896759034473417412 7874255812015493663938996905817738591654 0553567040928213322216314109787108145997 8669599704509681841906299443656015145490 4880922084480034822492077304030431884298 9939313526688234966210194716191070146196 8523192847482034495897709553561107027581 7487333272966789987984732840981907648512 7263100174016678736347760585724503696443 4897992034489997455662402937487668839751 4044516657077500605138839916688140725455 4466522205072426239237921152531816251253 6305093172863142200406457130527580230766 5183351995689139748137504926429605010013 651980186945639498

(или какому-нибудь другому подходящему, не менее внушительному по величине чи­слу). Это число, без сомнения, выглядит устрашающе большим! Оно, действительно, чрезвычайно велико, но я не вижу спосо­ба, как его можно было бы сделать мень­ше. Процедуры кодирования и определения, использованные мною для машин Тьюрин­га, вполне разумны и достаточно просты, и все же с неизбежностью приводят к подоб­ным несуразно большим числам для реаль­ной универсальной машины Тьюринга.

Я уже говорил, что все современные об­щеупотребительные компьютеры, по сути, являются универсальными машинами Тью­ринга. Я ни в коем случае не подразуме­ваю под этим, что их логическая структура должна в точности походить на предложен­ную мной выше структуру универсальной машины Тьюринга. Однако сутб дела состо­ит в том, что если сперва ввести в произ­вольную универсальную машину Тьюринга соответствующую программу (начало пода­ваемой на вход ленты), то потом она смо­жет копировать поведение любой машины Тьюринга! В предыдущем примере програм­ма просто принимает форму одного числа (числа п), но этим разнообразие возмож­ных процедур и вариантов исходной схемы Тьюринга отнюдь не исчерпывается. В дей­ствительности я сам, описывая машину, не­сколько отклонился от того, что исходно было предложено Тьюрингом. Но ни одно из этих отклонений не имеет сейчас для нас существенного значения.