РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ.
Рядом Тейлора для функции 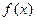 называется степенной ряд вида
называется степенной ряд вида
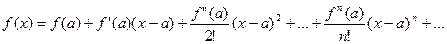
Если а=0, то получим частный случай ряда Тейлора
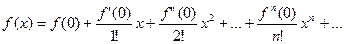
Который называется рядом Маклорена.
Степенной ряд внутри его промежутка сходимости можно почленно дифференцировать и интегрировать сколько угодно раз, причём полученные ряды имеют тот же промежуток сходимости, что и исходный ряд.
Два степенных ряда можно почленно складывать и умножать по правилам сложения и умножения многочленов. При этом промежуток сходимости полученного нового ряда совпадает с общей частью промежутков сходимости исходных рядов.
Для разложения функции 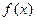 в ряд Маклорена необходимо:
в ряд Маклорена необходимо:
1) вычислить значения функции и её последовательных производных в точке х=0, т.е. 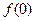 ,
, 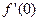 ,
, 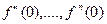
2) составить ряд Маклорена, подставив значения функции и её последовательных производных в формулу
3) найти промежуток сходимости полученного ряда по формуле
для разложения функции в ряд Тейлора необходимо:
1) Вычислить значения функции и её последовательных производных в точке х=а, т.е. 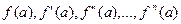
2) Составить ряд Тейлора, подставив значения функции и её последовательных производных в формулу.
3) Найти промежуток сходимости по формуле.
26. Разложить в ряд Маклорена функцию:
1) 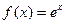 ; 2)
; 2) 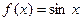 ; 3)
; 3) 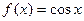 ; 4)
; 4) 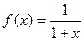 ;
;
5) 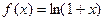 ; 6)
; 6) 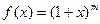 ; 7)
; 7) 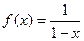 ; 8)
; 8) 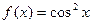 ;
;
9) 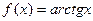 ; 10)
; 10) 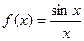 .
.
1) Вычислим значения функции и её производных при х=0; имеем 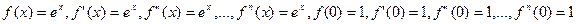 (n=1, 2, 3,…).
(n=1, 2, 3,…).
Подставив эти значения в формулу, получим разложение функции 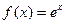 в ряд Маклорена:
в ряд Маклорена:
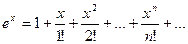
Этот ряд называется экспоненциальным рядом.
Промежуток сходимости найдём по формуле
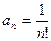 ;
; 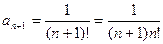 ;
; 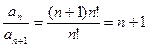
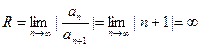 , т.е.
, т.е. 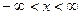 .
.
Полученный ряд сходится к функции 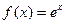 при любых значениях х, так как в любом промежутке функция
при любых значениях х, так как в любом промежутке функция 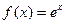 и её производные по абсолютной величине ограничены одним и тем же числом.
и её производные по абсолютной величине ограничены одним и тем же числом.
2) Вычислим значения функции и её производных при х=0, имеем 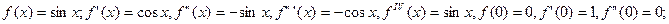
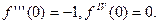 Заметим, что производные чётного порядка
Заметим, что производные чётного порядка 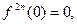 а производные нечетного порядка
а производные нечетного порядка 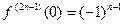 (n=1, 2, 3, 4, …)
(n=1, 2, 3, 4, …)
Подставив эти значения в формулу, получим разложение синуса в ряд Маклорена:
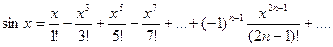
Промежуток сходимости полученного ряда найдём по формуле
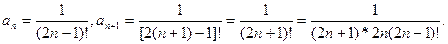
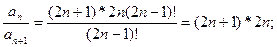
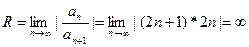 ,
,
Т.е. ряд сходится в промежутке 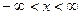 .
.
3) Рассуждая так же, как и в п. 2, аналогично получаем
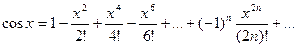
Причём этот ряд сходится в промежутке 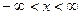 .
.
4) Вычислим значения функции и её производных при х=0; имеем 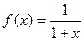
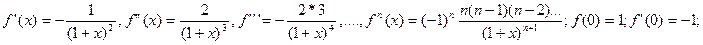
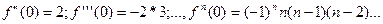
Подставив эти значения в формулу, получим разложение функции 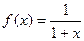 в ряд Маклорена:
в ряд Маклорена:
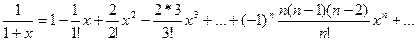
Или
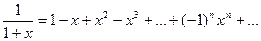
Промежуток сходимости найдём по формуле: 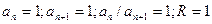 . Следовательно, -1<x<1.
. Следовательно, -1<x<1.
При х=-1 и х=1 ряд расходится, поэтому область сходимости ряда – промежуток -1<x<1.
5)I способ. Вычислим значения функции и её производных при х=0; имеем 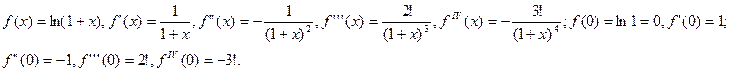 Отсюда следует, что
Отсюда следует, что
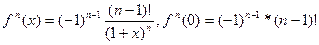 (n=1, 2, 3, 4, … )
(n=1, 2, 3, 4, … )
Подставив эти значения в формулу, получим разложение данной функции в ряд Маклорена:
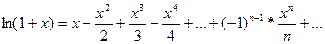
Этот ряд называется логарифмическим рядом.
Промежуток сходимости найдём по формуле: 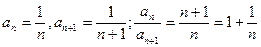 ,
,
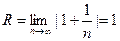 , т.е. -1<x<1.
, т.е. -1<x<1.
Исследуем сходимость ряда в точках x=-1 и x=1. При х=-1 ряд расходится как гармонический. При х=1 имеем знакочередующийся ряд
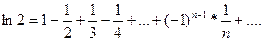 ,
,
Который сходится по признаку Лейбница. Итак, данный ряд сходится в промежутке -1<x<1.
Дата добавления: 2016-06-05; просмотров: 2176;










