В п. 1.2. рассматривали решение систем, у которых число уравнений совпадает с числом неизвестных и с определителем из коэффициентов, от-личным от нуля. Метод Гаусса – еще один способ решения, не требующий таких ограничений.
Рассмотрим систему
ï
ï
î
ï
ï
í
ì
=
+
+
+
=
+
+
+
=
+
+
+
m
n
mn
2
m2
1
m1
2
n
2n
2
22
1
21
1
n
1n
2
12
1
11
b
x
a
...
x
a
x
a
....
..........
..........
..........
..........
b
x
a
...
x
a
x
a
b
x
a
...
x
a
x
a
,
,
.
(1.7)
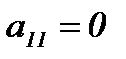Будем считать, что . Если , то перенумеровывая неиз-
вестные, получим первый коэффициент, отличный от нуля.
Умножим первое уравнение на 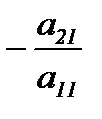и сложим почленно со вторым, затем первое умножим на 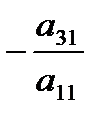и сложим с третьим. Продолжая этот процесс, получим равносильную систему при условии, что первое уравнение остается неизменным :
ï
ï
î
ï
ï
í
ì
¢
=
¢
+
+
¢
¢
=
¢
+
+
¢
=
+
+
+
,
b
x
a
...
a
....
..........
..........
..........
..........
,
b
x
a
...
x
a
,
b
x
a
...
x
a
x
a
m
n
mn
m
n
n
n
n
(1.8)
где 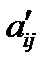- новые коэффициенты, 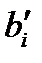- новые свободные члены.
Умножая второе уравнение на 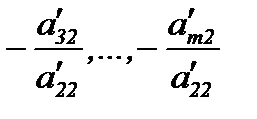и складывая с соответ-
ствующими уравнениями, получим систему
ï
ï
ï
î
ï
ï
ï
í
ì
¢ .
¢
=
¢
¢
+
+
¢
¢
¢
¢
=
¢
¢
+
+
¢
¢
¢
=
¢
+
+
¢
=
+
+
+
m
n
mn
3
m3
3
n
3n
3
33
2
n
2n
2
22
1
n
1n
2
12
1
11
b
x
a
...
x
a
........
..........
..........
..........
..........
,
b
x
a
...
x
a
,
b
x
a
...
x
a
,
b
x
a
...
x
a
x
a
(1.9)
Продолжая этот процесс, можем получить одну из следующих ситуаций:
1. Одно из уравнений системы имеет отличную от нуля правую часть и нулевые коэффициенты в левой. В этом случае система не имеет решений.
2. Система имеет вид
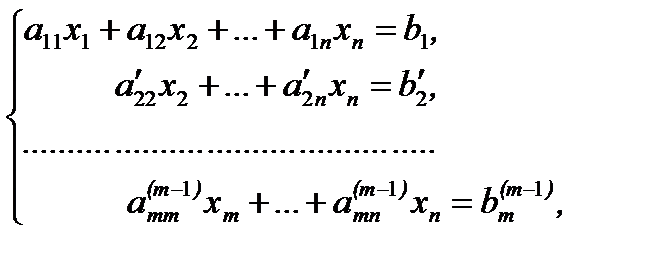
где
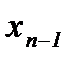Если m=n, то система совместна, имеет единственное решение. В этом случае из последнего уравнения определяется , из предпоследнего и так далее (обратный ход Гаусса).
Если m<n, то переменные 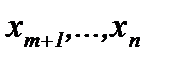- свободные переменные и, следо-вательно, переносятся в правую часть (см. п. 1.3.). Затем обратным ходом Гаусса переменные 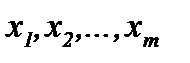выражаются через свободные переменные.
В процессе последовательного исключения неизвестных могут поя-виться уравнения 0=0. Эти уравнения отбрасываются.
На практике удобнее работать не c системой (1.7), а с ее расширенной матрицей, так как в рассмотренном процессе преобразовываются коэффи-циенты при неизвестных, в расширенной матрице при этом производятся элементарные преобразования со строками.
. Если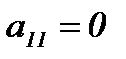 
, то перенумеровывая неиз-
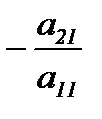и сложим почленно со вторым, затем первое умножим на 
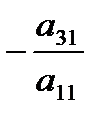и сложим с третьим. Продолжая этот процесс, получим равносильную систему при условии, что первое уравнение остается неизменным :
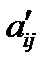- новые коэффициенты, 
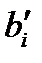- новые свободные члены.
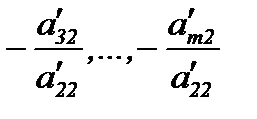и складывая с соответ-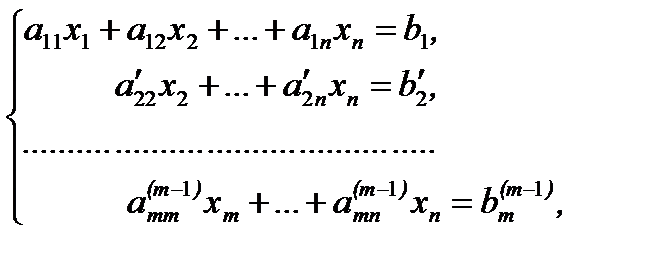
, из предпоследнего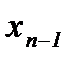 
и так далее (обратный ход Гаусса).
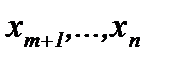- свободные переменные и, следо-вательно, переносятся в правую часть (см. п. 1.3.). Затем обратным ходом Гаусса переменные 
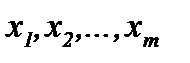выражаются через свободные переменные.
