Устойчивость линейных САР (САУ). Введение

Одной из основных задач ТАР является исследование динамических процессов, протекающих в САР. САР всегда подвержена действию всевозможных внешних возмущающих сил (сигналы управления, настройки, помехи и др.), которые могут вывести её из состояния равновесия. Если система устойчива, то она вернётся к исходному состоянию.

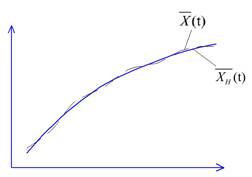С технической точки зрения требования к устойчивости системы являются более жёсткими, чем с математической, т.к. требует устойчивости не только как таковой, но требует и удовлетворения некоторых временных интервалов, в течение которых система должна восстановить устойчивость.

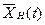- номинальный режим движения системы (предположим, три координаты и три скорости. Или шесть координат(ещё углы) и шесть скоростей),

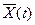- реальное (возмущённое) движение.

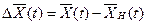- вектор приращений возмущений.

Для устойчивого движения объекта .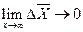

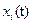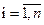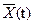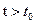Движение называется устойчивым по Ляпунову, если при небольших изменениях начальных значений , (что соответствует малым начальным возмущениям) возмущенное движение при к ак угодно мало отличается от невозмущенного движения 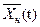(асимптотически устойчиво).

Исходные уравнения, как правило, в общем случае нелинейные. Чтобы воспользоваться теоремами устойчивости Ляпунова, эти уравнения необходимо линеаризовать.

Пусть 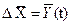или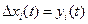

, (*)

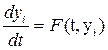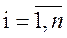Или в виде одного векторно-матричного уравнения:

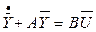, где 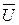- вектор управления.

Линеаризуем (*) в районе номинального значения (разложим в ряд Тейлора):

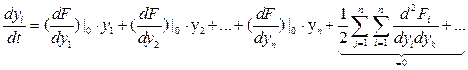
Индекс «0» означает, что линеаризация происходит в некоторой точке, где проводится анализ (если будет другая точка, то будут другие коэффициенты линеаризации и другое решение)

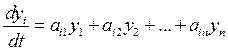(2*)

Коэффициенты 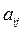зависят от параметров системы

1) Самый простой случай 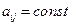- дифференциальное уравнение с постоянными коэффициентами (часто можно решить аналитически)

2) 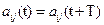- периодически меняющиеся коэффициенты. Есть методы определения аналитических решений (метод Рэлея, теория Флоке и т.д.)

3) 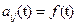- самый общий случай (только численное решение).

Условия, при которых можно использовать решение линеаризованных уравнений (*) при исследовании устойчивости движения без опаски ошибиться сформулированы Ляпуновым в следующих теоремах.

Теорема 1

Если все корни характеристического уравнения 1-го приближения имеют вещественные части отрицательные, то невозмущенное движение асимптотически устойчиво при малых отклонениях (устойчива «в малом»), независимо от отброшенных частей.

Теорема 2

Если среди корней 1-го приближения есть хотя бы один с положительной вещественной частью, то движение неустойчиво, независимо от отброшенной части.

Критический (сомнительный) случай

Если система имеет нулевой или чисто мнимые корни, а остальные отрицательные, то нельзя однозначно сказать об устойчивости, это пограничный случай. В этом случае необходимы дополнительные исследования с помощью отброшенных частей.

ВООБЩЕ:для нелинейных систем устойчивость «в малом» ещё не даёт гарантии устойчивости «в большом», т.е. при любых начальных отклонениях. Т.е. здесь устойчивость зависит от величины начальных возмущений. В линейных (линеаризованных) системах устойчивость не зависит от начальных возмущений.

При аналитическом исследовании динамических свойств системы (САР) необходимо найти её дифференциальное уравнение и затем проинтегрировать. Т.е. будет найден закон изменения во времени интересующей нас величины. Однако решение ДУ высоких порядков достаточно сложно. Поэтому очень важно научиться судить об устойчивости без непосредственного решения ДУ. В дальнейшем исследуем именно однородную систему (независящую от управления, а только лишь от своих параметров):

.

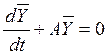Другая форма записи:

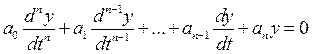(3*)

Где 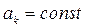- коэффициенты, определяемые параметрами системы.

Характеристическое уравнение:

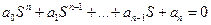(4*)

Обозначим корни данного характеристического уравнения 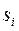. Тогда общее решение может быть записано так:

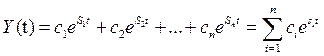. Постоянные интегрирования 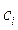зависят от начальных условий, наложенных на саму переменную и её производные.

Предположим, среди корней есть k- действительных корней и (n-k) – комплексных.

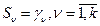
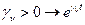- возрастает во времени и, следовательно, процесс неустойчивый.

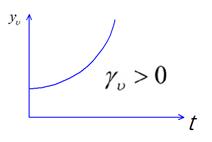
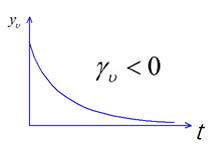
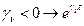- убывает во времени, процесс устойчивый.

Теперь комплексные корни:

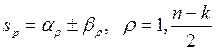
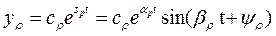. Возможны следующие варианты:

Устойчивый (сходящийся, затухающий) колебательный процесс

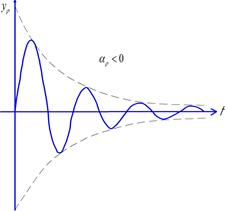
Неустойчивый (расходящийся) колебательный процесс

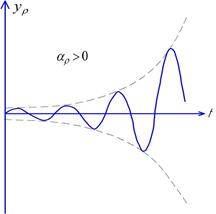
Чисто колебательный процесс

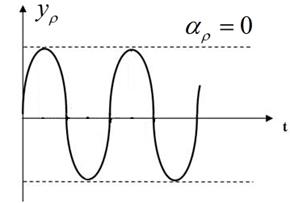
Все пограничные состояния системы будем относить к неустойчивому движению.

Часто удобно представить характерное уравнение в следующем виде:

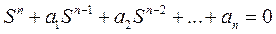
Если все корни найдены:

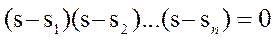
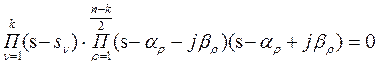
Важное значение приобретают правила, позволяющие определять устойчивость системы, минуя вычисление корней. Это правило называется критериями устойчивости.