Свойства скалярного произведения.
 (переместительный закон).
(переместительный закон).
 (распределительный закон).
(распределительный закон).
 (сочетательный закон).
(сочетательный закон).



Если два ненулевых вектора заданы своими координатами

 , то скалярное произведение этих двух векторов равно сумме произведений соответствующих координат:
, то скалярное произведение этих двух векторов равно сумме произведений соответствующих координат:
 (1)
(1)
Тогда из (6.1) и (6.2) следует, что
 (2)
(2)
При умножении вектора на число получается коллинеарный вектор.
Пусть  , тогда
, тогда

Признаком коллинеарности  двух векторов является пропорциональность их координат:
двух векторов является пропорциональность их координат:
 (3)
(3)
Признак ортогональности двух векторов можно получить из (2)
Если ^ , то j =p/2, cosj=0
 , т.е. xa×xb+ ya×yb+ za×zb=0.
, т.е. xa×xb+ ya×yb+ za×zb=0.
Пример 5. Найти скалярное произведение векторов
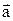 =(3; 5; 1) и
=(3; 5; 1) и 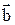 =(-1; 5; 2).
=(-1; 5; 2).
Используя формулу (2.8), получим
3(-1)+5×5+1×2=-3+25+2=24.
Пример. Найти угол между векторами
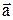 =(0; -1; +2) и
=(0; -1; +2) и 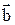 =(1; -2; 3).
=(1; -2; 3).
Получаем

4. Разложение вектора по ортам в пространстве R3
Рассмотрим декартову прямоугольную систему координат OXYZ в пространстве  , и произвольный радиус вектор
, и произвольный радиус вектор 
 |
 М3
М3
 |
 М
М
 | |||
 | |||
О М2
 |
М1
Р
Из точки M конца радиуса-вектора 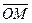 проведём прямую, параллельную оси OZ до пересечения в точке P с плоскостью OXY. Обозначим через M1 и M2 — соответственно, проекции точки P на оси OX и OY. Пусть M3 – проекция точки M на ось OZ. Тогда будем иметь
проведём прямую, параллельную оси OZ до пересечения в точке P с плоскостью OXY. Обозначим через M1 и M2 — соответственно, проекции точки P на оси OX и OY. Пусть M3 – проекция точки M на ось OZ. Тогда будем иметь

Заменив векторы  и
и  равными им векторами
равными им векторами  и
и  , получим
, получим
 (4)
(4)
Равенство (4) показывает, что всякий вектор в R3 можно представить в виде суммы трёх векторов, лежащих на осях координат. От точки O в направлении каждой оси отложим по вектору длины, равной 1. Обозначим эти вектора через  и
и  , соответственно и назовём их ортами. Обозначим через x, y и z — проекции вектора
, соответственно и назовём их ортами. Обозначим через x, y и z — проекции вектора 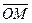 на координатные оси OX, OY и OZ, соответственно. Так как векторы
на координатные оси OX, OY и OZ, соответственно. Так как векторы  и
и  лежат на одной оси OX, то
лежат на одной оси OX, то  =
=  . Аналогично,
. Аналогично,  =
=  ,
,  =
=  . Следовательно, равенство (4) может быть переписано в виде
. Следовательно, равенство (4) может быть переписано в виде
 (5)
(5)
Равенство (2.2) даёт разложение вектора 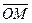 по ортам
по ортам 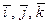 . Вместо полной записи (2.2) часто пользуются сокращенной
. Вместо полной записи (2.2) часто пользуются сокращенной 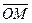 ={x, y, z }, где x, y, z — проекции вектора
={x, y, z }, где x, y, z — проекции вектора 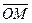 на координатные оси, которые будем называть координатами вектора
на координатные оси, которые будем называть координатами вектора 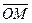 .
.
Дата добавления: 2021-11-16; просмотров: 96;










