Психофизические шкалы. Функция желательности Харрингтона. Обобщенная функция желательности
Нередко при оценивании альтернатив возникает необходимость в использовании измерений с помощью специально разрабатываемых вербально-числовых шкал, применяемых преимущественно в случаях, когда оценки носят субъективный характер, в частности, при экспертном оценивании. Эти шкалы носят название психофизических и позволяют формализовать имеющуюся у эксперта систему предпочтений.
Психофизические шкалы задаются функциями специального вида — функциями желательности и устанавливают соответствие между натуральными значениями показателей в физических шкалах и психофизическими параметрами — субъективными оценками «ценности» этих значений. Обычно функцию желательности d(x) строят таким образом, чтобы в наиболее распространенной области «удовлетворительно» она была близка к линейной и в то же время изменялась от 0 до 1 на всем возможном множестве значений показателя. Понятно, что при таком подходе к нормированию функция желательности должна быть более «чувствительна» к изменению значений информативного показателя x в области «удовлетворительно» и менее чувствительна вне ее.
Наиболее известной и часто используемой является функция желательности Харрингтона, впервые примененная им в задачах контроля качества массовой продукции. Шкала Харрингтона устанавливает соответствие между лингвистическими оценками желательности значений показателя х и числовыми интервалами d(х) (табл. 2.2):
Таблица 2.2
Числовые интервалы шкалы Харрингтона
| Лингвистическая оценка | Интервалы значений функции желательности d(x) |
| Очень хорошо | 1,00-0,80 |
| Хорошо | 0,80-0,63 |
| Удовлетворительно | 0,63-0,37 |
| Плохо | 0,37-0,20 |
| Очень плохо | 0,20-0,00 |
При таком шкалировании значения функции желательности d(x) изменяются в интервале от 0 до 1, причем значение di»0 соответствует абсолютно неприемлемой величине i-го показателя качества жизни, di»1 — идеальной величине.
Практически часто ограничиваются тремя градациями шкалы Харрингтона, отвечающим лингвистическим категориям «плохо», «удовлетворительно», «хорошо». В это случае область, соответствующая уровню «удовлетворительно», расширяется от 0,37 до 0,69, а области «плохо» и «хорошо» характеризуются интервалами (0,00-0,37) и (0,69-1,00) соответственно.
Аналитически для монотонных по предпочтениям критериев, характерных, например, для показателей качества жизни, функция желательности Харрингтона задается следующей формулой:
di = d (zi) = exp (-exp (-zi)), (2.3)
zi = (хi – хi0)/( хi1 – хi0), (2.4)
где zi — кодированные значения i-го показателя, представляющие собой безразмерные величины; хi — значение i-го информативного показателя; хi0 и хi1 — границы области «удовлетворительно» в исходной шкале:
di0= d (zi (хi0)) = 0,37; di1= d (zi (хi1)) = 0,69. (2.5)
Функция желательности Харрингтона представляет собой монотонно возрастающую функцию, изменяющуюся от 0 до 1.
При кодированном значении информативного показателя z=0 (нижняя граница области «удовлетворительно») функция желательности принимает значение 0,368, при z=1, т.е. нижняя граница области «удовлетворительно», d(z)=0,692. Для ее построения достаточно, чтобы эксперты указали границы исходных показателей хi0 и хi1, внутри которых качество жизни можно считать удовлетворительным. В частности, можно эти значения положить равными хi1=хmax и хi0=хmin, т.е. соответственно максимальному и минимальному значению показателя по массиву региональных данных.
Приведем пример. Максимальная величина показателя «Число студентов на 1000 населения» в 1998 г. по выборке регионов Центрального федерального округа, исключая данные для г. Москвы, наблюдалась для Орловской области: хmax=26,9, минимальная хmin=12,2 — для Владимирской. Принимая вышеприведенное определение границ области «удовлетворительно», получаем: хi1=26,9 и хi0=12,2. Тогда безразмерная переменная z будет представлять собой ни что иное, как определенный по методике Программы развития ООН, модифицированной для регионов, индекс образования, вычисляемый по формуле:
индекс = (х – хmin)/( хmax – хmin), (2.6)
где х — значение информативного показателя для региона; хmax и хmin — соответственно максимальное и минимальное значения показателя по массиву региональных данных.
Значения функции желательности для Владимирской и Орловской областей примут значения d(z)=0,368 и 0,692 соответственно. В то же время для Москвы как субъекта Федерации, для которой безразмерная переменная z=4,21, функции желательности составляет d(4,21)=0,985 — значение, достаточно близкое к единице.
На рис. 2.1 представлены результаты сопоставления значений частного индекса образования и соответствующих величин функции желательности для регионов ЦФО, включая г. Москву (метки регионов проставлены лишь для некоторых из них).
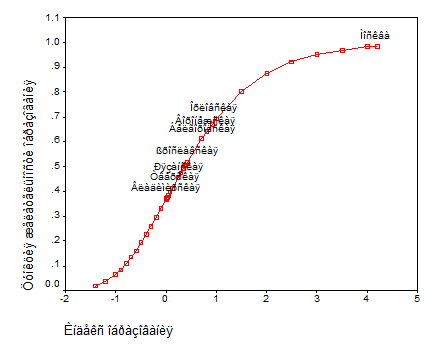
Рис. 2.1. Функция желательности Харрингтона для индекса образования
Из рис. 2.1 видно, что значения индекса образования практически линейно связаны с реально достижимыми величинами функции желательности, отвечающими интервалу значений индекса образования от 0 до 1, и лишь выше и существенно ниже интервала «удовлетворительно» четко просматривается нелинейность этой взаимосвязи. Заметим также, что крутизна зависимости функции желательности от индекса образования в области «плохо» заметно больше крутизны кривой в области «хорошо». Этот факт является отражением математических свойств функции Харрингтона, важных в аспекте ее использования в целях управления.
Введение шкалы желательности позволяет свести исходную многокритериальную задачу принятия решения с разноразмерными критериями к многокритериальной задаче с критериями, измеряемыми в одной и той же шкале, поэтому следующим этапом является свертка частных функций желательности di в обобщенный критерий D.
Обобщенный критерий рекомендуется выбирать из семейства средних по Колмогорову, задаваемых монотонными функциями y. Выбор этих функций осуществляется с привлечением суждений экспертов о связи обобщенного критерия с величинами частных функций желательности. Так, логично предположить, что совершенно неудовлетворительная ситуация по одному критерию (di»0) влечет за собой неудовлетворительную оценку ситуации в целом (D»0). В математической форме это суждение находит свое отражение с помощью функций вида:
y1 = ln d, (2.7)
y2 = -ln (-ln d), (2.8)
Соответствующие обобщенные критерии равны среднему геометрическому
D1 = DG = exp (S1/n* ln di) = (d1 d2 … dn)1/n, (2.9)
и среднему логарифмическому
D1 = DL = exp [-(-ln d1)(-ln d2)…(-ln dn)1/n] . (2.10)
Если частные критерии неравноценны, то их весовые коэффициенты различны между собой, и обобщенные критерии имеют следующий вид:
D1 = DG = exp (S1/n* ln di) = d1a1 d2a2 … dnan, (2.11)
D1 = DL = exp [-(-ln d1)a1(-ln d2)a2…(-ln dn)an] . (2.12)
Сравнение критериев DG и DL показывает, что обобщенный критерий DG дает более жесткую оценку, чем DL: DG £ DL во всей области определения частных функций желательности.
Помимо выбора вида свертки частных функций желательности в обобщенный критерий, важной задачей является назначение весовых коэффициентов. Один из эффективных методов экспертного оценивания весов — метод аналитических иерархий, логические и алгоритмические основы которого будут рассмотрены в лекции 3.
Дата добавления: 2018-05-10; просмотров: 2226;










