Магнитодвижущая сила фазы

При прохождении тока по обмотке образуется магнитодвижущая сила (МДС), которая зависит от устройства обмотки и протекающих по ней токов.

Предположим, что на статоре двухполюсной машины в пазах размещена катушка с числом витков w_к и шагом y=τ_п. Ротор машины представляет собой цилиндр. Воздушный зазор между статором и ротором равномерный. Если по катушке пропустить синусоидальный ток i_к = √2 I_к sin ωt , где ω=2πf – угловая частота сети, то он создаст магнитное поле, линии которого показаны на рис. 2.1.

Распределение МДС катушки на двух полюсных делениях показано на рис. 2.2, где изображена развертка статора. МДС катушки имеет прямоугольную форму.

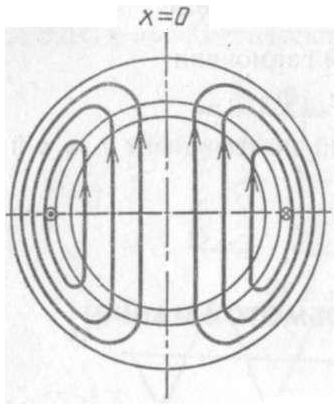
Рис. 2.1. Магнитное поле катушки при y = τ_п

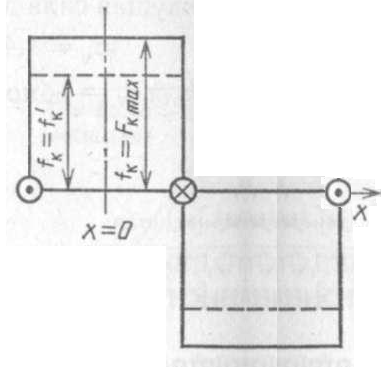
Рис. 2.2. Магнитодвижущая сила катушки при y = τ_п для двух моментов времени

Для различных моментов времени в соответствии с изменением мгновенного значения тока МДС, оставаясь неподвижной в пространстве, будет изменять свое значение и направление согласно уравнению

f_к = F_кmax sin ωt,

где 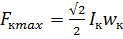— максимальное значение МДС катушки на один полюс.

Для удобства анализа прямоугольную МДС заменяют суммой гармоник (рис. 2.3).

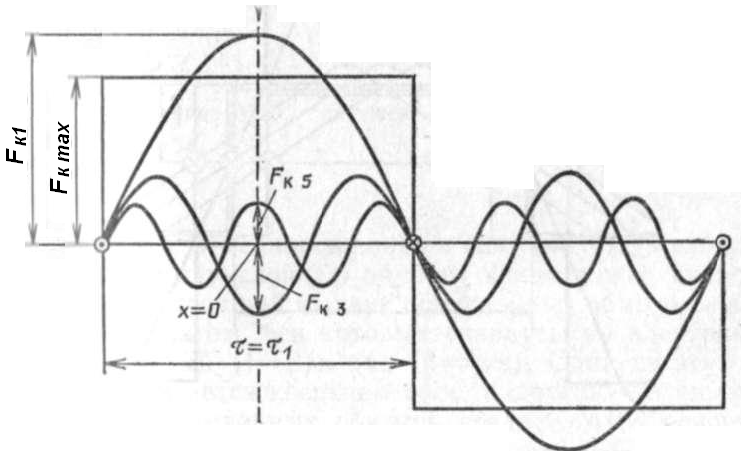
Рис. 2.3. Разложение МДС катушки в гармонический ряд

Если ось катушки принять за начало отсчета, то МДС 1-й гармоники в любой точке полюсного деления, расположенной на расстоянии х от оси катушки, будет равна:

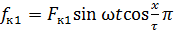,(2.1)

где F_к1 = 0,9 I_к w_к.

Уравнение (2.1) является математическим выражением волны, пульсирующей во времени по синусоидальному закону и распределённой в пространстве также по синусоидальному закону.

Высшие гармоники МДС оказывают вредное влияние на работу машины и поэтому их стараются ослабить. Для уменьшения МДС высших гармоник и за счёт этого приближения кривой результирующей МДС к синусоидальной обмотку выполняют с укорочением шага и распределяют ее по пазам.

Если катушечная группа состоит из q пространственно смещенных одинаковых катушек с диаметральным шагом, то результирующую МДС фазы на полюсном делении получим суммированием прямоугольных МДС катушек (рис. 2.4).

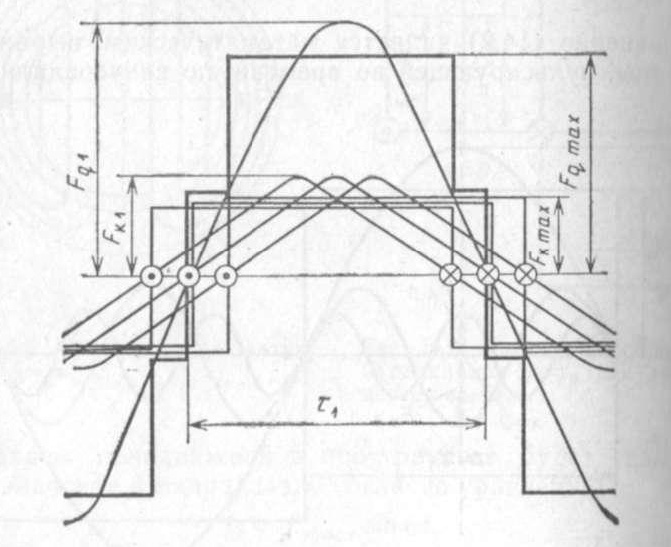
Рис. 2.4. МДС q катушек обмотки при y = τ_п

Результирующая кривая МДС представляет собой ступенчатую фигуру, которая с увеличением q по форме будет приближаться к синусоиде. Разложим прямоугольные кривые катушек в гармонический ряд.

Максимальное значение МДС фазы для 1-й гармоники F_q1 равно :

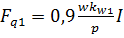, (2.2)

где k_w1 – обмоточный коэффициент, который учитывает распределение обмотки по пазам, укороченный шаг обмотки и наличие скоса пазов; w – витки фазы; I – ток фазы.

Основная гармоника МДС в точке х полюсного деления для любого момента времени будет равна:

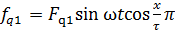, (2.3)

где координата х отсчитывается от оси катушечной группы.

Основная гармоника МДС фазы неподвижна в пространстве, имеет синусоидальное пространственное распределение и пульсирует во времени.

Пульсирующую МДС можно представить в виде двух вращающихся в противоположных направлениях волн. Используя известное тригонометрическое преобразование, для основной гармоники МДС (2.3), получаем

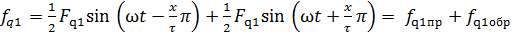, (2.4)

где f_q1пр – МДС прямо вращающейся волны; f_q1обр – МДС обратно вращающейся волны.

Составляющие в правой части (2.4) представляют собой уравнения синусоидально распределенных в пространстве вращающихся волн. С возрастанием времени вращающиеся волны перемещаются, перемещаются и их амплитуды.

Окружная скорость прямо вращающейся волны

v_пр1=ωτ/π=2τf . (2.5)

Окружная скорость обратно вращающейся волны

v_пр1=-ωτ/π=-2τf . (2.6)

Скорости перемещения пространственных синусоидальных волн одинаковые, но имеют противоположные знаки.

Частота вращения магнитных полей будет равна:

n=60f/p.