Лекция 9 Формула Стокса.
Ротор векторного поля.
Назовем ротором векторного поля 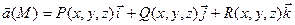 вектор
вектор
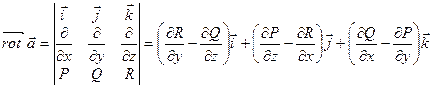
Свойства ротора.
1) Линейность 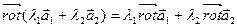
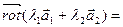
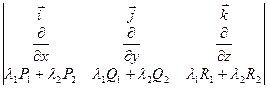 =
= 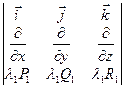 +
+
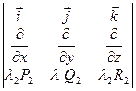 =
= 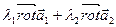 .
.
2) 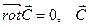 - постоянное векторное поле.
- постоянное векторное поле.
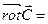
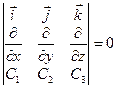
3) 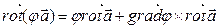
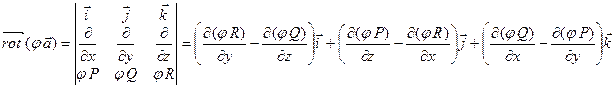 =
=
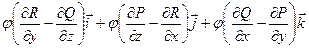 +
+ 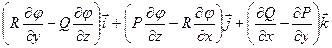 =
= 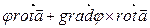 .
.
Теорема Стокса.
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность 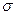 с кусочно-гладкой границей
с кусочно-гладкой границей 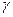 .
.
Пусть компоненты векторного поля 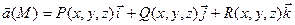 непрерывны и имеют непрерывные частные производные по своим аргументам до второго порядка включительно в области V.
непрерывны и имеют непрерывные частные производные по своим аргументам до второго порядка включительно в области V.
Тогда справедлива формула Стокса
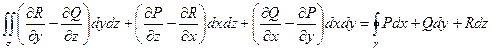
Замечание. Нормаль к поверхности 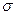 проведена так, чтобы наблюдатель, находясь на конце вектора нормали, видел бы обход контура
проведена так, чтобы наблюдатель, находясь на конце вектора нормали, видел бы обход контура 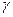 , совершающимся в положительном направлении (так, чтобы область, границей которой является контур, при обходе контура находилась бы «по левую руку»).
, совершающимся в положительном направлении (так, чтобы область, границей которой является контур, при обходе контура находилась бы «по левую руку»).
Доказательство теоремы Стокса.
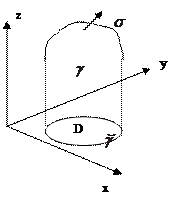 
| Как и формула Остроградского – Гаусса, формула Стокса состоит из трех независимых частей (в силу произвольности компонент векторного поля). Докажем одну из этих частей, остальные формулы доказываются аналогично. Докажем 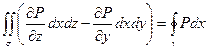 - часть формулы Стокса, в которой содержится только компонента P.
Предположим, что поверхность - часть формулы Стокса, в которой содержится только компонента P.
Предположим, что поверхность 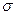 описывается уравнением описывается уравнением 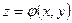 . Тогда нормаль к поверхности . Тогда нормаль к поверхности
|
представляет собой вектор 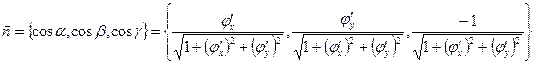
Отсюда видно, что 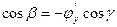 . Вспомним еще, что
. Вспомним еще, что 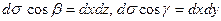 .
.
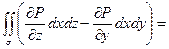
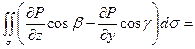
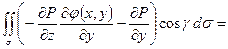
(на поверхности 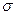
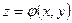 , поэтому под интегралом стоит частная производная P по y с учетом зависимости z от y на поверхности
, поэтому под интегралом стоит частная производная P по y с учетом зависимости z от y на поверхности 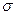 )
)
= 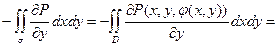
Используем формулу Грина для области D с ее границей 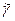 . Ее можно записать в виде
. Ее можно записать в виде
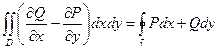 . Нам понадобится только та ее часть, которая относится к функции P
. Нам понадобится только та ее часть, которая относится к функции P 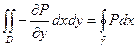 . Продолжаем равенство дальше.
. Продолжаем равенство дальше.
= 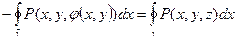 .
.
В самом деле, на контуре 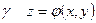 , а переменные x, y на том и другом контуре те же, так как контур
, а переменные x, y на том и другом контуре те же, так как контур 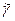 - это проекция контура
- это проекция контура 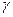 на плоскость OXY (параллельно оси OZ).
на плоскость OXY (параллельно оси OZ).
Одна из частей формулы Стокса доказана.
Линейным интеграломвекторного поля 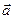 по дуге L называется криволинейный интеграл
по дуге L называется криволинейный интеграл 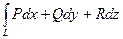 .
.
Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляциейвекторного поля называется линейный интеграл по замкнутому контуру.
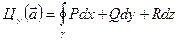 .
.
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
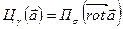 .
.
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора.
Рассмотрим произвольную точку M в области V. Проведем через нее поверхность 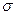 , границей которой служит контур
, границей которой служит контур 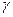 . Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим
. Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим
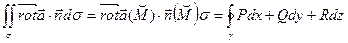 .
.
Здесь, как и ранее 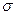 - обозначение области и ее площади. Из этого соотношения, стягивая контур
- обозначение области и ее площади. Из этого соотношения, стягивая контур 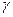 к точке M, получим
к точке M, получим
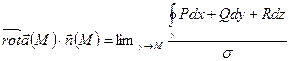
Это и есть инвариантное определение ротора.
Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором 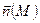 ). Левая часть – это проекция ротора на это направление.
). Левая часть – это проекция ротора на это направление.
Если направление 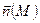 совпадает с направлением ротора и
совпадает с направлением ротора и 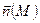 - единичный вектор, то левая часть равна модулю ротора. Поэтому модуль ротора векторного поля равен максимальному значению поверхностной плотности циркуляции векторного поля.
- единичный вектор, то левая часть равна модулю ротора. Поэтому модуль ротора векторного поля равен максимальному значению поверхностной плотности циркуляции векторного поля.
Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая.
Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью 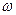
Векторное поле линейной скорости 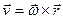 .
.
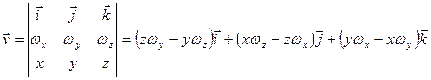 ,
,
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.
Дата добавления: 2017-11-21; просмотров: 2934;










